如图1,在Rt△ABC中,∠ABC=90°,D为AC中点,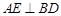 于
于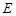 (不同于点
(不同于点 ),延长AE交BC于F,将△ABD沿BD折起,得到三棱锥
),延长AE交BC于F,将△ABD沿BD折起,得到三棱锥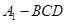 ,如图2所示.
,如图2所示.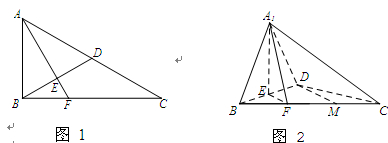
(1)若M是FC的中点,求证:直线 //平面
//平面 ;
;
(2)求证:BD⊥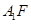 ;
;
(3)若平面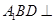 平面
平面 ,试判断直线
,试判断直线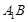 与直线CD能否垂直?并说明理由.
与直线CD能否垂直?并说明理由.
在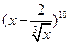 的展开式中,(1)写出展开式中含
的展开式中,(1)写出展开式中含 的项;(2)如果第
的项;(2)如果第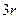 项和第
项和第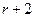 项的二项式系数相等,求
项的二项式系数相等,求 的值.
的值.
有红色和黑色两个盒子,红色盒子中有大小、形状相同的球6个,其中1个标有数字0,2个标有数字1,3个标有数字2,黑色盒子中有大小、形状相同的球7个,其中4个标有数字0,1个标有数字1,2个标有数字2,现从红色的盒子中任取1个球(每个球被取到的可能性相等),黑色的盒 子中任取2个球(每个球被取到的可能性相等),共3个球。
子中任取2个球(每个球被取到的可能性相等),共3个球。
(1)求取出的3个球都标有数字0的概率;
(2)求取出的3个球数字之积为4的概率;
(3)求取出的3个球数字之积为0的概率。
从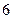 名上海世博会志愿者中选
名上海世博会志愿者中选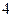 人分别到世博会园区内的德国国家馆、日本国家馆、意大利国家馆、瑞典国家馆服务,要求每个场馆安排
人分别到世博会园区内的德国国家馆、日本国家馆、意大利国家馆、瑞典国家馆服务,要求每个场馆安排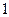 人。
人。
(1)这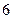 人中甲必须去,共有多少种不同的安排方案?
人中甲必须去,共有多少种不同的安排方案?
(2)这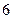 人中甲、乙两人不去日本国家馆,共有多少种不同的安排方案?
人中甲、乙两人不去日本国家馆,共有多少种不同的安排方案?
已知函数 的最大值为2。
的最大值为2。
(1)求 的值及
的值及 的最小正周期;
的最小正周期;
(2)求 的单调递增区间
的单调递增区间
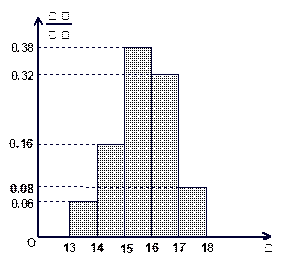
某班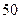 名学生在一次百米测试中,成绩全部介于
名学生在一次百米测试中,成绩全部介于 秒与
秒与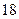 秒之间,将测
秒之间,将测 试结果按如下方式分成五组:第一组
试结果按如下方式分成五组:第一组 ,第二组
,第二组 ,…,第五组
,…,第五组 ,下图是按上述分组方法得到的频率分布直方图。
,下图是按上述分组方法得到的频率分布直方图。
(1)若成绩大于或等于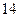 秒且小于
秒且小于 秒认为良好,求该班在这次百米测试中成绩良好的人数;
秒认为良好,求该班在这次百米测试中成绩良好的人数;
(2)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于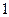 的概率。
的概率。