选做题.(本小题满分10分.请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.作答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑.)
.在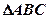 中,已知
中,已知 是
是 的角平分线,
的角平分线, 的外接圆交
的外接圆交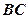 于点
于点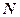 ,
,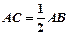 .求证:
.求证: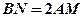 .
.
已知函数 ,若
,若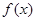 的最大值为1
的最大值为1
(Ⅰ)求 的值,并求
的值,并求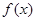 的单调递增区间;
的单调递增区间;
(Ⅱ)在 中,角
中,角 、
、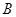 、
、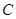 的对边
的对边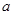 、
、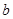 、
、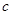 ,若
,若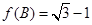 ,且
,且 ,试判断三角形的形状.
,试判断三角形的形状.
为了对某课题进行研究,用分层抽样方法从三所科研单位A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人):
| 科研单位 |
相关人数 |
抽取人数 |
| A |
16 |
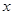 |
| B |
12 |
3 |
| C |
8 |
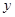 |
(Ⅰ)确定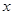 与
与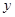 的值;
的值;
(Ⅱ)若从科研单位A、C抽取的人中选2人作专题发言,求这2人都来自科研单位A的概率.
已知 .
.
(Ⅰ)求函数 在
在 上的最小值;
上的最小值;
(Ⅱ)对一切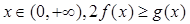 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(Ⅲ)证明:对一切 ,都有
,都有 成立.
成立.
已知抛物线 的焦点为F2,点F1与F2关于坐标原点对称,以F1,F2为焦点的椭圆C过点
的焦点为F2,点F1与F2关于坐标原点对称,以F1,F2为焦点的椭圆C过点 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设点
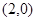 ,过点F2作直线
,过点F2作直线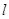 与椭圆C交于A,B两点,且
与椭圆C交于A,B两点,且 ,若
,若 的取值范围.
的取值范围.
已知数列 满足
满足 ,
, (
(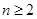 且
且 ).
).
(Ⅰ)求数列 的通项公式
的通项公式 ;
;
(Ⅱ)令 ,记数列
,记数列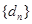 的前
的前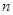 项和为
项和为 ,若
,若 恒为一个与
恒为一个与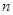 无关的常数
无关的常数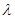 ,试求常数
,试求常数 和
和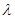 .
.