如图,在某点B处测得建筑物AE的顶端A的仰角为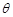 ,沿BE方向前进30m,至点C处测得顶端A的仰角为2
,沿BE方向前进30m,至点C处测得顶端A的仰角为2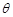 ,再继续前进10
,再继续前进10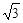 m至D点,测得顶端A的仰角为4
m至D点,测得顶端A的仰角为4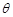 ,求建筑物AE的高度。
,求建筑物AE的高度。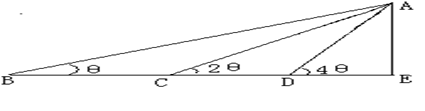
已知中心在原点的椭圆C: 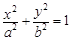 的一个焦点为
的一个焦点为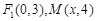
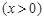 为椭圆C上一点,△MOF2的面积为
为椭圆C上一点,△MOF2的面积为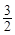 .
.
(1)求椭圆C的方程;
(2)是否存在平行于OM的直线l,使得l与椭圆C相交于A、B两点,且以线段AB为直径的圆恰好过原点?若存在,求出直线l的方程;若不存在,说明理由.
某校高三有四个班,某次数学测试后,学校随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人. 抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中120~130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.
(1)问各班被抽取的学生人数各为多少人?
(2)求平均成绩;
(3)在抽取的所有学生中,任取一名学生,求分数不低于90分的概率.
先后抛掷一枚骰子,得到的点数分别记为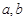 ,按以下程序进行运算:
,按以下程序进行运算:
(1)若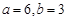 ,求程序运行后计算机输出的y的值;
,求程序运行后计算机输出的y的值;
(2)若“输出y的值是3”为事件A,求事件A发生的概率.
已知函数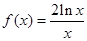
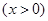
(1)求函数 在
在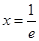 处的切线的斜率;
处的切线的斜率;
(2)求函数 的最大值;
的最大值;
(3)设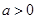 ,求函数
,求函数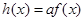 在
在 上的最大值.
上的最大值.
已知阶矩阵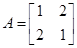 ,向量
,向量 。
。
(1)求阶矩阵 的特征值和特征向量;
的特征值和特征向量;
(2)计算 .
.