已知点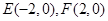 ,曲线
,曲线 上的动点
上的动点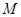 满足
满足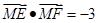 ,定点
,定点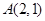 ,由曲线
,由曲线 外一点
外一点 向曲线
向曲线 引切线
引切线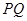 ,切点为
,切点为 ,且满足
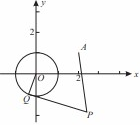
,且满足 .
.
(1)求线段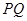 长的最小值;
长的最小值;
(2)若以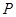 为圆心所作的圆
为圆心所作的圆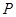 与曲线
与曲线 有公共点,试求半径取最小值时圆
有公共点,试求半径取最小值时圆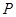 的标准方程.
的标准方程.
定理:若函数 在闭区间[m,n]上是连续的单调函数,且
在闭区间[m,n]上是连续的单调函数,且 ,则存在唯一一个
,则存在唯一一个 。已知
。已知
(1)若 是减函数,求a的取值范围。
是减函数,求a的取值范围。
(2)是否存在 同时成立,若存在,指出c、d之间的等式关系,若不存在,请说明理由。
同时成立,若存在,指出c、d之间的等式关系,若不存在,请说明理由。
已知函数 时取最大值2。
时取最大值2。 是集合
是集合 中的任意两个元素,
中的任意两个元素, 的最小值为
的最小值为 。
。
(1)求a、b的值;
(2)若 的值。
的值。
已知圆C:x2+y2+2x-4y+3=0,若圆C的切线在x轴和y轴上的截距绝对值相等,求切线方程.
实数a,b,c满足条件3(a2+b2)=4c2(c≠0).
(1)求证:直线ax+by+c=0与圆x2+y2=1交于不同的两点P、Q;
(2)求弦PQ的长.
已知圆的方程是x2+y2=2,直线y=x+b,当b为何值时,圆与直线有两个公共点?