一个袋中装有10个大小相同的小球.其中白球5个、黑球4个、红球1个.
(1)从袋中任意摸出2个球,求至少得到1个白球的概率;
(2)从袋中任意摸出3个球,记得到白球的个数为 ,求随机变量
,求随机变量 的数学期望
的数学期望 .
.
已知双曲线C: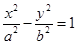 (a>b>0)的一个焦点为
(a>b>0)的一个焦点为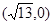 ,离心率为
,离心率为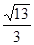 .
.
(1)求双曲线C的标准方程;
(2)若动点P(x0,y0)为双曲线外一点,且点P到双曲线C的两条切线相互垂直,求点P的轨迹方程。
数列{an}满足a1+2a2+22a3+…+2n-1an=4n.
⑴求通项an;
⑵求数列{an}的前n项和 Sn.
已知向量 =(sin(
=(sin(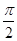 +x),
+x),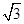 cosx),
cosx), =(sinx,cosx), f(x)=
=(sinx,cosx), f(x)=  ·
· .
.
⑴求f(x)的最小正周期和单调增区间;
⑵如果三角形ABC中,满足f(A)=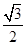 ,求角A的值.
,求角A的值.
在 中,角
中,角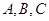 的对边分别为
的对边分别为 ,
, 的外接圆半径
的外接圆半径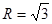 ,且满足
,且满足
(1)求角 和边
和边 的大小;
的大小;
(2)求 的面积的最大值。
的面积的最大值。
已知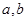 为正整数(
为正整数(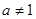 ),等差数列
),等差数列 的首项为
的首项为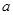 ,公差为
,公差为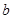 , 等比数列
, 等比数列 的首项为
的首项为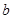 ,公比为
,公比为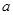 .满足条件
.满足条件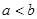 ,且
,且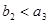 .在数列
.在数列 与
与 中各存在一项
中各存在一项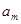 与
与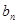 有
有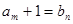 ,又设
,又设 .
.
(1)求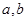 的值.
的值.
(2)若数列 为等差数列,求常数
为等差数列,求常数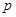 .
.