如图,椭圆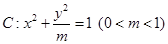 的左顶点为
的左顶点为 ,
, 是椭圆
是椭圆 上异于点
上异于点 的任意一点,点
的任意一点,点 与点
与点 关于点
关于点 对称.
对称.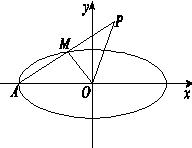
(1)若点 的坐标为
的坐标为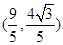 ,求
,求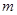 的值;
的值;
(2)若椭圆 上存在点
上存在点 ,使得
,使得 ,求
,求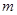 的取值范围.
的取值范围.
已知椭圆的中心在原点,焦点为F1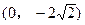 ,F2(0,
,F2(0, ),且离心率
),且离心率 。
。
(1)求椭圆的方程;
(2)直线 (与坐标轴不平行)与椭圆交于不同的两点A、B,且线段AB中点的横坐标为
(与坐标轴不平行)与椭圆交于不同的两点A、B,且线段AB中点的横坐标为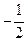 ,求:直
,求:直 线斜率的取值范围。
线斜率的取值范围。
、如图,四棱锥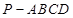 中,底面ABCD为矩形,
中,底面ABCD为矩形,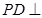 底面ABCD,AD=PD=1,AB=
底面ABCD,AD=PD=1,AB=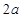 (
(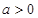 ),E,F分别CD,PB的中点。
),E,F分别CD,PB的中点。
(1)求证:EF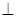 平面PAB;,
平面PAB;,
(2)当 时,求AC与平面AEF所成角的正弦值。
时,求AC与平面AEF所成角的正弦值。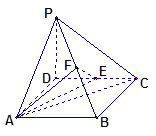
已知空间三点A(0,2,3),B(-2,1,6),C(1,-1,5)
求:⑴求以向量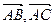 为一组邻边的平行四边形的面积S;
为一组邻边的平行四边形的面积S;
⑵若向量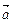 分别与向量
分别与向量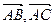 垂直,且|
垂直,且|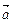 |=
|= ,求向量
,求向量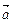 的坐标。
的坐标。
抛物线 的焦点为F,点A、B在抛物线上(A点在第一象限,B点在第四象限),且|FA|=2,|FB|=5,
的焦点为F,点A、B在抛物线上(A点在第一象限,B点在第四象限),且|FA|=2,|FB|=5,
求:(1)点A、B的坐标
(2)线段AB的长度和直线AB的方程;
若椭圆 =1(a>b>0)与直线
=1(a>b>0)与直线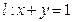 在第一象限内有两个不同的交点,求a、b所满足的条件,并画出点P(a,b)的存在区域。
在第一象限内有两个不同的交点,求a、b所满足的条件,并画出点P(a,b)的存在区域。