设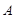 是同时符合以下性质的函数
是同时符合以下性质的函数 组成的集合:
组成的集合:
①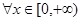 ,都有
,都有 ;②
;② 在
在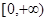 上是减函数.
上是减函数.
(1)判断函数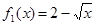 和
和 (
( )是否属于集合
)是否属于集合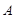 ,并简要说明理由;
,并简要说明理由;
(2)把(1)中你认为是集合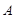 中的一个函数记为
中的一个函数记为 ,若不等式
,若不等式 对任意的
对任意的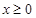 总成立,求实数
总成立,求实数 的取值范围.
的取值范围.
(本题满分13分) 已知圆C:x2+y2+2x-4y+3=0.
(1)若不过原点的直线l与圆C相切,且在x轴,y轴上的截距相等,求直线l的方程;
(2)从圆C外一点P(x,y)向圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求点P的轨迹方程.
(本题满分13分) 在△ABC中,A,B,C分别是三边a,b,c的对角.设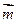 =(cos,sin),
=(cos,sin), =(cos,-sin),
=(cos,-sin), ,
, 的夹角为. (1)求C的大小;(2)已知c=,三角形的面积S = ,求a +b的值.
的夹角为. (1)求C的大小;(2)已知c=,三角形的面积S = ,求a +b的值.
(本小题满分12分)已知函数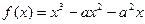 .(Ⅰ)若
.(Ⅰ)若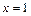 时函数
时函数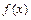 有极值,求
有极值,求 的值;(Ⅱ)求函数
的值;(Ⅱ)求函数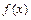 的单调增区间;(Ⅲ)若方程
的单调增区间;(Ⅲ)若方程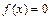 有三个不同的解,分别记为
有三个不同的解,分别记为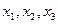 ,证明:
,证明: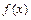 的导函数
的导函数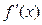 的最小值为
的最小值为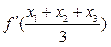 .
.
(本小题满分12分)已知二次函数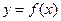 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为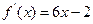 ,数列
,数列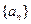 的前n项和为
的前n项和为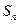 ,点
,点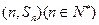 均在函数
均在函数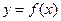 的图像上。(Ⅰ)求数列
的图像上。(Ⅰ)求数列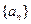 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设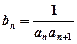 ,
,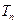 是数列
是数列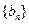 的前n项和,求使得
的前n项和,求使得 对所有
对所有 都成立的最小正整数m.
都成立的最小正整数m.
(本小题满分12分)设数列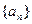 的前n项和为Sn=2n2,
的前n项和为Sn=2n2,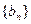 为等比数列,且
为等比数列,且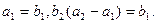 (Ⅰ)求数列
(Ⅰ)求数列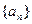 和
和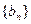 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前n项和Tn.
的前n项和Tn.