某公司2011年利润为100万元,因市场竞争,若不开发新项目,预测从2012年起每年利润比上一年减少4万元.2012年初,该公司一次性投入90万元开发新项目,预测在未扣除开发所投入资金的情况下,第n年(n为正整数,2012年为第一年)的利润为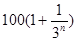 万元.
万元.
(1)设从2012年起的前n年,该公司不开发新项目的累计利润为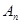 万元,开发新项目的累计利润为
万元,开发新项目的累计利润为 万元(须扣除开发所投入资金),求
万元(须扣除开发所投入资金),求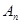 ,
, 的表达式.
的表达式.
(2)依上述预测,该公司从第几年开始,开发新项目的累计利润超过不开发新项目的累计利润?
设等差数列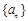 的前
的前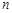 项和为
项和为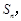 且
且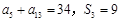 .
.
(1)求数列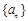 的通项公式及前
的通项公式及前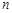 项和公式;
项和公式;
(2)设数列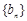 的通项公式为
的通项公式为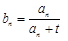 ,问: 是否存在正整数t,使得
,问: 是否存在正整数t,使得
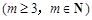 成等差数列?若存在,求出t和m的值;若不存在,请说明理由.
成等差数列?若存在,求出t和m的值;若不存在,请说明理由.
在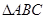 中,
中,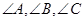 所对的边分别是
所对的边分别是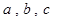 ,不等式
,不等式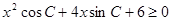 对一切实数
对一切实数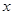 恒成立.
恒成立.
(1)求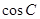 的取值范围;
的取值范围;
(2)当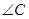 取最大值,且
取最大值,且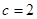 时,求
时,求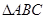 面积的最大值并指出取最大值时
面积的最大值并指出取最大值时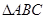 的形状
的形状
设数列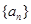 的前n项和为
的前n项和为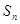 ,且
,且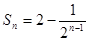 ,数列
,数列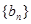 为等差数列,且
为等差数列,且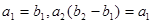 .
.
(1)求数列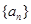 和
和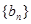 的通项公式;(2)设
的通项公式;(2)设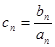 ,求数列
,求数列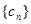 的前n项和
的前n项和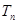 .
.
在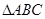 中,若
中,若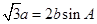 .
.
(1)求角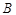 的大小;
的大小;
(2)若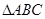 是锐角三角形,且
是锐角三角形,且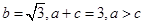 求
求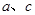 的值
的值