已知函数 .
.
(1)当 时,求
时,求 在
在 最小值;
最小值;
(2)若 存在单调递减区间,求
存在单调递减区间,求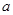 的取值范围;
的取值范围;
(3)求证: (
(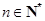 ).
).
如图,设四棱锥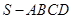 的底面为菱形,且∠
的底面为菱形,且∠ ,
,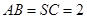 ,
,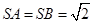 。
。
(1)求证:平面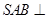 平面
平面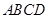 ;
;
(2)设P为SD的中点,求三棱锥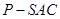 的体积.
的体积.
(本小题满分12分)已知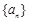 是正项数列,
是正项数列,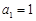 ,且点
,且点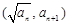 (
(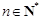 )在函数
)在函数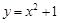 的图像上.
的图像上.
(1)求数列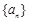 的通项公式;
的通项公式;
(2)若列数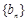 满足
满足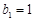 ,
, ,求证:
,求证: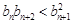 .
.
(本小题满分10分)选修4—5:不等式选讲
已知函数f(x)=|2x-1|+|2x+a|,g(x)=x+3.
(1)当a=-2时,求不等式f(x)<g(x)的解集;
(2)设a>-1,且当x∈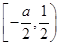 时,f(x)≤g(x),求a的取值范围.
时,f(x)≤g(x),求a的取值范围.
(本小题满分10分)选修4—4:坐标系与参数方程
已知曲线C1的参数方程为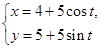 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sin θ.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sin θ.
(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π).
(本小题满分10分)选修4—1:几何证明选讲
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.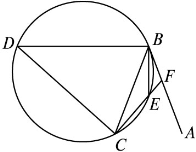
(1)证明:DB=DC;
(2)设圆的半径为1,BC=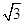 ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.