甲、乙两人参加某种选拔测试.在备选的10道题中,甲答对其中每道题的概率都是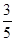 ,乙能答对其中的5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,得分最低为0分,至少得15分才能入选.
,乙能答对其中的5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,得分最低为0分,至少得15分才能入选.
(Ⅰ)求乙得分的分布列和数学期望;
(Ⅱ)求甲、乙两人中至少有一人入选的概率.
若电灯B可在桌面上一点O的垂线上移动,桌面上有与点O距离为 的另一点A,问电灯与点0的距离怎样,可使点A处有最大的照度?(
的另一点A,问电灯与点0的距离怎样,可使点A处有最大的照度?( 照度与
照度与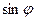 成正比,与
成正比,与 成反比)
成反比)
某人定制了一批地砖. 每块地砖 (如图1所示)是边长为 米的正方形
米的正方形 ,点E、F分别在边BC和CD上, △
,点E、F分别在边BC和CD上, △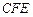 、△
、△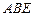 和四边形
和四边形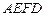 均由单一材料制成,制成△
均由单一材料制成,制成△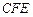 、△
、△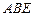 和四边形
和四边形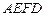 的三种材料的每平方米价格之比依次为3:2:1. 若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分成四边形
的三种材料的每平方米价格之比依次为3:2:1. 若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分成四边形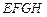 .
.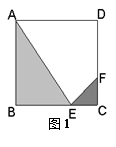
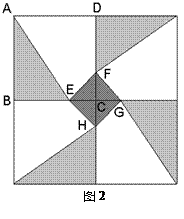
(1) 求证:四边形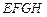 是正方形;
是正方形;
(2)  在什么位置时,定制这批地砖所需的材料费用最省?
在什么位置时,定制这批地砖所需的材料费用最省?
某产品按质量分为10个档次,生产第一档(即最低档次)的利润是每件8元,每提高一个档次,利润每件增加2元,但在相同的时间内产量减少3件.在相同的时间内,最低档的产品可生产60件.问在相同的时间内,生产第几档次的产品的总利润最大?有多少元?
请您设计一个帐篷。它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如右图所示)。试问当帐篷的顶点O到底面中心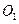 的距离为多少时,帐篷的体积最大?
的距离为多少时,帐篷的体积最大?
路灯距地平面为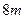 ,一个身高为
,一个身高为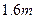 的人以
的人以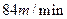 的速率在地面上行走,从路灯在地平面上射影点C,沿某直线离开路灯,求人影长度的变化速率v.
的速率在地面上行走,从路灯在地平面上射影点C,沿某直线离开路灯,求人影长度的变化速率v.