设函数f(x)=
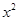 +ax-lnx(a∈R).
+ax-lnx(a∈R).
(Ⅰ)当a=1时,求函数f(x)的极值;
(Ⅱ)当a≥2时,讨论函数f(x)的单调性;
(Ⅲ)若对任意 及任意
及任意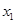 ,
,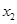 ∈[1,2],恒有
∈[1,2],恒有 成立,求实数m的取值范围.
成立,求实数m的取值范围.
如图,在直棱柱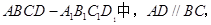

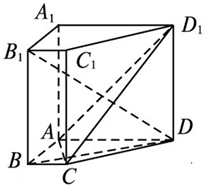
(1)证明: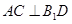 ;
;
(2)求直线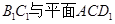 所成角的正弦值.
所成角的正弦值.
设关于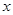 的一元二次方程
的一元二次方程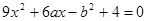 .
.
(1)若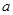 是从1,2,3这三个数中任取的一个数,
是从1,2,3这三个数中任取的一个数,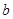 是从0,1,2这三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2这三个数中任取的一个数,求上述方程有实根的概率;
(2)若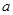 是从区间[0,3]中任取的一个数,
是从区间[0,3]中任取的一个数,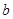 是从区间[0,2]中任取的一个数,求上述方程有实根的概率.
是从区间[0,2]中任取的一个数,求上述方程有实根的概率.
已知命题
命题
若命题“ ”是真命题,求实数
”是真命题,求实数 的取值范围.
的取值范围.
已知定义域为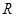 的函数
的函数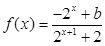 是奇函数.
是奇函数.
(1)求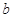 的值;
的值;
(2)判断函数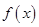 的单调性并证明;
的单调性并证明;
(3)若对任意的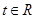 ,不等式
,不等式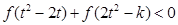 恒成立,求
恒成立,求 的取值范围
的取值范围
(本小题满分12分)斜三棱柱 中,侧面
中,侧面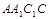
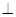 底面ABC,侧面
底面ABC,侧面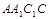 是菱形,
是菱形,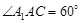 ,
,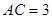 ,
,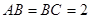 ,E、F分别是
,E、F分别是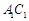 ,AB的中点.
,AB的中点.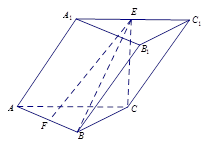
(1)求证:EF∥平面 ;
;
(2)求证:CE⊥面ABC.
(3)求四棱锥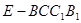 的体积.
的体积.