一个多面体的直观图、正视图、侧视图、俯视图如图所示,M、N分别为A1B、B1C1的中点.

(1)求证:MN//平面ACC1A1;
(2)求证:MN^平面A1BC.
如图,在四棱锥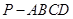 中,
中,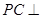 底面
底面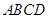 ,
,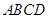 是直角梯形,
是直角梯形, ,
,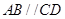 ,
,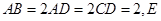 是
是 的中点。
的中点。
(1)求证:平面 平面
平面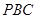
(2)若二面角 的余弦值为
的余弦值为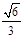 ,求直线
,求直线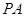 与平面
与平面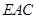 所成角的正弦值.
所成角的正弦值.
某篮球队甲、乙两名队员在本赛季已结束的8场比赛中得分统计的茎叶图如下: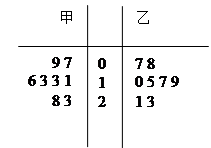
(1)比较这两名队员在比赛中得分的均值和方差的大小;
(2)以上述数据统计甲、乙两名队员得分超过15分的频率作为概率,假设甲、乙两名队员在同一场比赛中得分多少互不影响,预测在本赛季剩余的2场比赛中甲、乙两名队员得分均超过15分的次数 的分布列和均值.
的分布列和均值.
已知数列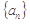 满足
满足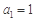 ,且
,且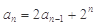 (n
(n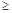 2且n∈N*).
2且n∈N*).
(Ⅰ)求数列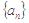 的通项公式;
的通项公式;
(Ⅱ)设数列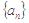 的前n项之和
的前n项之和 ,求
,求 ,并证明:
,并证明: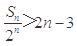 .
.
设函数
(I)画出函数 的图象;
的图象;
(II)若不等式, 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
在平面直角坐标系xOy中,以O为极点,X轴的正半轴为极轴,取与直角坐标系相同的长度单位建立极坐标系.曲线C1的参数方程为: (
( 为参数);射线C2的极坐标方程为:
为参数);射线C2的极坐标方程为: ,且射线C2与曲线C1的交点的横坐标为
,且射线C2与曲线C1的交点的横坐标为
(I )求曲线C1的普通方程;
(II)设A、B为曲线C1与y轴的两个交点,M为曲线C1上不同于A、B的任意一点,若直线AM与MB分别与x轴交于P,Q两点,求证|OP|.|OQ|为定值.