某校内有一块以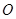
为圆心，
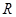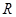（为常数，单位为米）为半径的半圆形（如图）荒地，该校总务处计划对其开发利用，其中弓形
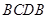区域（阴影部分）用于种植学校观赏植物，
区域用于种植花卉出售，其余区域用于种植草皮出售.已知种植学校观赏植物的成本是每平方米20元，种植花卉的利润是每平方米80元，种植草皮的利润是每平方米30元.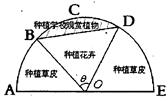
（1）设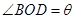
（单位：弧度），用
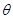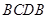表示弓形的面积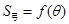
；
（2）如果该校总务处邀请你规划这块土地，如何设计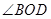
的大小才能使总利润最大？并求出该最大值.
（参考公式：扇形面积公式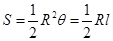
，
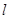表示扇形的弧长）
（本小题满分12分）已知8支球队中有3支弱队，以抽签方式将这8支球队分为A、B两组，每组4支．求：
（1）A、B两组中有一组恰有两支弱队的概率；
（2）A组中至少有两支弱队的概率．
（本小题满分12分）甲、乙两人各进行一次射击，如果两人击中目标的概率都是0．6，计算：
（1）两人都击中目标的概率；
（2）其中恰有一人击中目标的概率；
（3）至少有一人击中目标的概率．
（本小题满分10分）一名学生在军训中练习射击项目，他射击一次，命中目标的概率是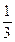
，若连续射击6次，且各次射击是否命中目标相互之间没有影响．
（1）求这名学生在第3次射击时，首次命中目标的概率；
（2）求这名学生在射击过程中，恰好命中目标3次的概率．
（本小题满分14分） 对于函数f（x），
若存在x0∈R，使f（x0）=x0成立， 则称x0为f（x）的不动点. 已知函数f（x）=ax2+（b+1）x+b－1（a≠0）
（1）当a=1，b=－2时，求f（x）的不动点；
（2）若对于任意实数b，函数f（x）恒有两个相异的不动点，求a的取值范围
（本小题满分13分）某车间生产某机器的两种配件A和B，生产配件A成本费y
与该车间的工人人数x成反比，而成生产配件B成本费y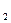
与该车间的工人人数x成正比，如果该车间的工人人数为10人时，这这两项费用y和y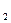分别为2万元和8万元，那么要使这两项费用之和最小，该车间的工人人数x应为多少