(本小题满分14分) 对于函数f(x), 若存在x0∈R,使f(x0)=x0成立, 则称x0为f(x)的不动点. 已知函数f(x)=ax2+(b+1)x+b-1(a≠0)
若存在x0∈R,使f(x0)=x0成立, 则称x0为f(x)的不动点. 已知函数f(x)=ax2+(b+1)x+b-1(a≠0)
(1)当a=1,b=-2时,求f(x)的不动点;
(2)若对于任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围
已知⊙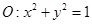 和点
和点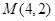 .
.
(Ⅰ)过点 向⊙
向⊙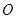 引切线
引切线 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)求以点 为圆心,且被直线
为圆心,且被直线 截得的弦长为4的⊙
截得的弦长为4的⊙ 的方程;
的方程;
(Ⅲ)设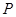 为(Ⅱ)中⊙
为(Ⅱ)中⊙ 上任一点,过点
上任一点,过点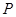 向⊙
向⊙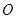 引切线,切点为
引切线,切点为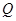 . 试探究:平面内是否存在一定点
. 试探究:平面内是否存在一定点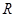 ,使得
,使得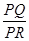 为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
设二次函数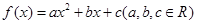 满足下列条件:
满足下列条件:
①当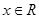 时,
时, 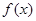 的最小值为0,且
的最小值为0,且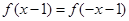 恒成立;
恒成立;
②当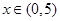 时,
时,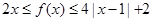 恒成立.
恒成立.
(I)求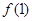 的值;
的值;
(Ⅱ)求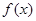 的解析式;
的解析式;
(Ⅲ)求最大的实数m(m>1),使得存在实数t,只要当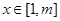 时,就有
时,就有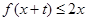 成立
成立
建造一条防洪堤,其断面为等腰梯形,腰与底边成角为 (如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为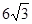 平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段
平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段 与两腰长的和)要最小.
与两腰长的和)要最小.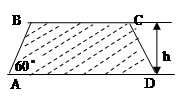
(1)求外周长的最小值,并求外周长最小时防洪堤高h为多少米?
(2)如防洪堤的高限制在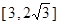 的范围内,外周长最小为多少米?
的范围内,外周长最小为多少米?
已知函数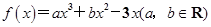 在点
在点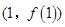 处的切线方程为
处的切线方程为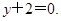
(1)求函数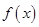 的解析式;
的解析式;
(2)若对于区间[-2,2]上任意两个自变量的值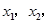 都有
都有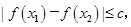 求实数c的最小值.
求实数c的最小值.
已知向量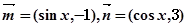
(1)当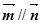 时,求
时,求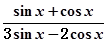 的值;
的值;
(2)设函数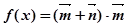 ,求
,求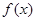 的单调增区间;
的单调增区间;
(3)已知在锐角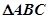 中,
中,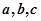 分别为角
分别为角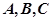 的对边,
的对边,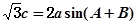 ,对于(2)中的函数
,对于(2)中的函数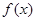 ,求
,求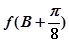 的取值范围。
的取值范围。