已知函数y＝x－1，令x＝―4,―3,―2,－1,0,1,2,3,4，可得函数图象上的九个点，在这九个点中随机取出两个点P1(x1,y1),P2(x2,y2)，
（1）求P1,P2两点在双曲线xy＝6上的概率；
（2）求P1,P2两点不在同一双曲线xy＝k(k≠0)上的概率。
（本小题满分12分）已知椭圆
的离心率为
，且抛物线
的焦点恰好是椭圆C的一个焦点.
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点
作直线
与椭圆C交于A，B两点，点N满足
（O为原点），求四边形OANB面积的最大值，并求此时直线的方程.
（本小题满分12分）
某单位开展岗前培训期间，甲乙2人参加了次考试，成绩统计如下表：
| 第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
|
| 甲的成绩 |
82 |
82 |
79 |
95 |
87 |
| 乙的成绩 |
95 |
75 |
80 |
90 |
85 |
（Ⅰ）根据有关统计知识，回答问题：
若从甲、乙2人中选出1人上岗，你认为选谁合适，请说明理由；
（Ⅱ）根据有关概率知识，解答下列问题：
①从甲、乙2人的成绩中各随机抽取一个，设抽到甲的成绩为x，抽取乙的成绩为y，用A表示满足条件
的事件，求事件A的概率；
②若一次考试两人成绩之差的绝对值不超过3分，则称该次考试两人“水平相当”，由上述5次成绩统计，任意抽查两次考试，求恰有一次考试两人“水平相当”的概率.
（本小题满分12分）如图所示，在四棱锥
中，底面ABCD为菱形，
，Q为AD的中点.
（Ⅰ）若
，求证：平面
平面
；
（Ⅱ）点M在线段PC上，二面角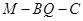
为
，若平面
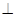平面ABCD，且
，
求三棱锥
的体积.
（本小题满分12分）在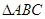
中，角A，B，C所对的边分别为a，b，c，已知
.
（Ⅰ）求C；
（Ⅱ）若
，
，且
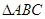，求的面积.
（本小题满分10分）【选修4-5：不等式选讲】
在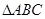
中，内角A、B、C所对的边的长分别为a、b、c，证明：
（Ⅰ）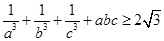
；
（Ⅱ）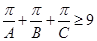
.