(本小题满分12分)已知椭圆
 的离心率为
的离心率为 ,且抛物线
,且抛物线 的焦点恰好是椭圆C的一个焦点.
的焦点恰好是椭圆C的一个焦点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点 作直线
作直线 与椭圆C交于A,B两点,点N满足
与椭圆C交于A,B两点,点N满足 (O为原点),求四边形OANB面积的最大值,并求此时直线
(O为原点),求四边形OANB面积的最大值,并求此时直线 的方程.
的方程.
数列 的各项均为正数,
的各项均为正数,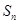 为其前
为其前 项和,对于任意的
项和,对于任意的 ,总有
,总有 成等差数列.
成等差数列.
(1)求 ;
;
(2)求数列 的通项公式;
的通项公式;
(3)设数列 的前
的前 项和为
项和为 ,且
,且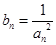 ,求证:对任意正整数
,求证:对任意正整数 ,总有
,总有
在边长为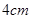 的正方形
的正方形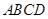 中,
中,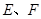 分别为
分别为 的中点,
的中点,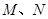 分别为
分别为 的中点,现沿
的中点,现沿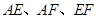 折叠,使
折叠,使 三点重合,重合后的点记为
三点重合,重合后的点记为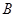 ,构成一个三棱锥.
,构成一个三棱锥.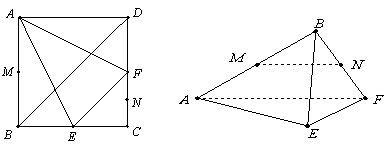
(1)请判断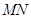 与平面
与平面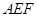 的位置关系,并给出证明;
的位置关系,并给出证明;
(2)证明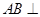 平面
平面 ;
;
(3)求四棱锥 的体积.
的体积.
为了对某课题进行研究,用分层抽样方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
| 高校 |
相关人数 |
抽取人数 |
| A |
18 |
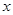 |
| B |
36 |
2 |
| C |
54 |
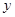 |
(1)求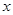 ,
,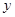 ;
;
(2)若从高校B、C抽取的人中选2人作专题发言,
求这2人都来自高校C的概率.
已知函数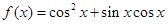 ,
,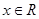
(1)求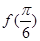 的值;
的值;
(2)若 ,且
,且 ,求
,求 .
.
已知函数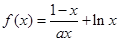
(1)当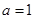 时,求
时,求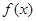 在
在 上的最小值;
上的最小值;
(2)若函数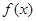 在
在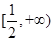 上为增函数,求正实数
上为增函数,求正实数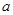 的取值范围;
的取值范围;
(3)若关于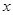 的方程
的方程 在区间
在区间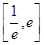 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数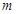 的取值范围.
的取值范围.