(本小题满分12分)
某单位开展岗前培训期间,甲乙2人参加了次考试,成绩统计如下表:
| |
第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
| 甲的成绩 |
82 |
82 |
79 |
95 |
87 |
| 乙的成绩 |
95 |
75 |
80 |
90 |
85 |
(Ⅰ)根据有关统计知识,回答问题:
若从甲、乙2人中选出1人上岗,你认为选谁合适,请说明理由;
(Ⅱ)根据有关概率知识,解答下列问题:
①从甲、乙2人的成绩中各随机抽取一个,设抽到甲的成绩为x,抽取乙的成绩为y,用A表示满足条件 的事件,求事件A的概率;
的事件,求事件A的概率;
②若一次考试两人成绩之差的绝对值不超过3分,则称该次考试两人“水平相当”,由上述5次成绩统计,任意抽查两次考试,求恰有一次考试两人“水平相当”的概率.
有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下 联表:
联表:
| 优秀 |
非优秀 |
合计 |
|
| 甲班 |
30 |
||
| 乙班 |
50 |
||
| 合计 |
200 |
已知全部200人中随机抽取1人为优秀的概率为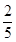
(1)请完成上面 联表;
联表;
(2)根据列联表的数据,能否有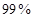 的把握认为“成绩与班级有关系”
的把握认为“成绩与班级有关系”
(3)从全部200人中有放回抽取3次,每次抽取一人,记被抽取的3人中优秀的人数为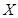 ,若每次抽取得结果是相互独立的,求
,若每次抽取得结果是相互独立的,求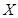 的分布列,期望
的分布列,期望 和方差
和方差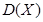
参考公式与参考数据如下:
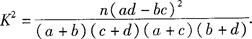
已知函数 ,
, ,若函数
,若函数 在
在 处的切线方程为
处的切线方程为 ,
,
(1)求 的值;
的值;
(2)求函数 的单调区间。
的单调区间。
延迟退休年龄的问题,近期引发社会的关注.人社部于2012年7月25日上午召开新闻发布会表示,我国延迟退休年龄将借鉴国外经验,拟对不同群体采取差别措施,并以“小步慢走”的方式实施.推迟退休年龄似乎是一种必然趋势,然而反对的声音也随之而起.现对某市工薪阶层关于“延迟退休年龄”的态度进行调查,随机抽取了50人,他们月收入的频数分布及对“延迟退休年龄”反对的人数
| 月收入(元) |
[1000,2000) |
[2000,3000) |
[3000,4000) |
[4000,5000) |
[5000,6000) |
[6000,7000) |
| 频数 |
5 |
10 |
15 |
10 |
5 |
5 |
| 反对人数 |
4 |
8 |
12 |
5 |
2 |
1 |
(1)由以上统计数据估算月收入高于4000的调查对象中,持反对态度的概率;
(2)若对月收入在[1000,2000),[4000,5000)的被调查对象中各随机选取两人进行跟踪调查,记选中的4人中赞成“延迟退休年龄”的人数为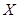 ,求
,求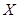 的分布列和数学期望.
的分布列和数学期望.
已知函数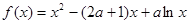
(1) 当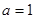 时, 求函数
时, 求函数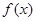 的单调增区间;
的单调增区间;
(2)当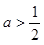 时,求函数
时,求函数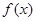 在区间
在区间 上的最小值;
上的最小值;
已知函数 ,其中
,其中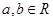
(1)若曲线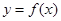 在点
在点 处的切线方程为
处的切线方程为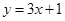 ,求函数
,求函数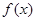 的解析式;
的解析式;
(2)讨论函数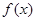 的单调区间;
的单调区间;