一个袋子装有大小形状完全相同的9个球,其中5个红球编号分别为1,2,3,4,5,4个白球编号分别为1,2,3,4,从袋中任意取出3个球.
(Ⅰ)求取出的3个球编号都不相同的概率;
(Ⅱ)记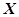 为取出的3个球中编号的最小值,求
为取出的3个球中编号的最小值,求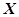 的分布列与数学期望.
的分布列与数学期望.
设函数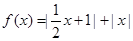
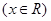 的最小值为a.
的最小值为a.
(Ⅰ)求a;
(Ⅱ)已知两个正数m,n满足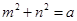 ,求
,求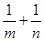 的最小值.
的最小值.
以直角坐标系的原点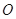 为极点,
为极点,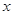 轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线
轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线 的参数方程为
的参数方程为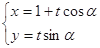 (
(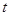 为参数,
为参数,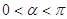 ),曲线
),曲线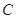 的极坐标方程为
的极坐标方程为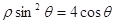 .
.
(Ⅰ)求曲线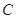 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线 与曲线
与曲线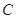 相交于
相交于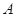 、
、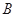 两点,当
两点,当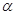 变化时,求
变化时,求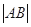 的最小值.
的最小值.
如图,已知直线PA与圆O相切于点A,经过点O的割线PBC交圆O于点B和点C,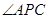 的平分线分别交AB,AC于点D和E.
的平分线分别交AB,AC于点D和E.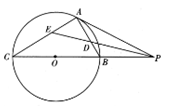
(Ⅰ)证明: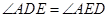 ;
;
(Ⅱ)若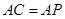 ,求
,求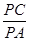 的值.
的值.
【改编】(本小题满分12分)已知函数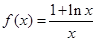 .
.
(Ⅰ)设 ,若函数
,若函数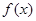 在区间
在区间 上存在极值,求实数a的取值范围;
上存在极值,求实数a的取值范围;
(Ⅱ)如果当 时,不等式
时,不等式 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.