【改编】(本小题满分12分)已知函数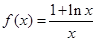 .
.
(Ⅰ)设 ,若函数
,若函数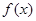 在区间
在区间 上存在极值,求实数a的取值范围;
上存在极值,求实数a的取值范围;
(Ⅱ)如果当 时,不等式
时,不等式 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
已知:函数f(x)=x -bx+3,且f(0)=f(4)。
-bx+3,且f(0)=f(4)。
(1)求函数y=f(x)的零点,写出满足条件f(x)<0的x的集合;
(2)求函数y=f(x)在区间[0,3]上的最大值和最小值。
已知:函数f(x)= +lg(3
+lg(3 -9)的定义域为A,集合B=
-9)的定义域为A,集合B= ,
,
(1)求:集合A;
(2)求:A B。
B。
(本小题满分10分)
对于在区间 上有意义的两个函数
上有意义的两个函数 和
和 ,如果对于任意的
,如果对于任意的 ,都有
,都有 ,则称
,则称 与
与 在区间
在区间 上是“接近”的两个函数,否则称它们在
上是“接近”的两个函数,否则称它们在 上是“非接近”的两个函数。现有两个函数
上是“非接近”的两个函数。现有两个函数 ,给定一个区间
,给定一个区间 。
。
(1)若 与
与 在区间
在区间 都有意义,求实数
都有意义,求实数 的取值范围;
的取值范围;
(2)讨论 与
与 在区间
在区间 上是否是“接近”的两个函数。
上是否是“接近”的两个函数。
(本小题满分10分)
已知:向量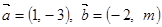 ,且
,且 。
。
(1)求实数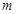 的值;
的值;
(2)当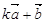 与
与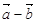 平行时,求实数
平行时,求实数 的值。
的值。
(本小题满分10分)
已知:向量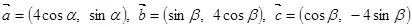
(1)若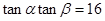 ,求证:
,求证: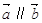 ;
;
(2)若 垂直,求
垂直,求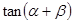 的值;
的值;
(3)求 的最大值。
的最大值。