已知抛物线 ,点
,点 ,过
,过 的直线
的直线 交抛物线
交抛物线 于
于 两点.
两点.
(1)若线段 中点的横坐标等于
中点的横坐标等于 ,求直线
,求直线 的斜率;
的斜率;
(2)设点 关于
关于 轴的对称点为
轴的对称点为 ,求证:直线
,求证:直线 过定点.
过定点.
已知命题p:方程 在[-1,1]上有且仅有一解.命题q:对于任意实数x都不满足不等式
在[-1,1]上有且仅有一解.命题q:对于任意实数x都不满足不等式 .若命题“p或q”是假命题,求a的取值范围.
.若命题“p或q”是假命题,求a的取值范围.
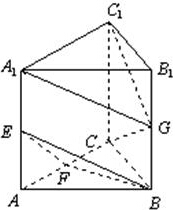
如图,在直三棱柱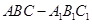 中,
中,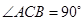 ,
,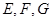 分别是
分别是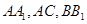 的中点,且
的中点,且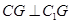 .
.
(Ⅰ)求证: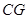 ∥平面
∥平面 ;
;
(Ⅱ)求证:平面 ⊥平面
⊥平面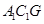 .
.
某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件.已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元,现该公司至少要生产A类产品50件,B类产品140件,求所需租赁费最少为多少元?
已知圆C经过两点P(-1,-3),Q(2,6),且圆心在直线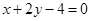 上,直线l的方程为
上,直线l的方程为 .
.
(1)求圆C的方程;
(2)证明:直线l与圆C恒相交;
(3)求直线l被圆C截得的最短弦长.
一质点运动的方程为s=8-3t2.
(1)求质点在[1,1+△t]这段时间内的平均速度;
(2)用定义法求质点在t=1时的瞬时速度.