如图,已知直线PA与圆O相切于点A,经过点O的割线PBC交圆O于点B和点C,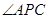 的平分线分别交AB,AC于点D和E.
的平分线分别交AB,AC于点D和E.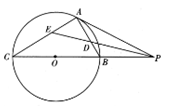
(Ⅰ)证明: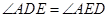 ;
;
(Ⅱ)若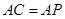 ,求
,求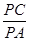 的值.
的值.
已知 ,
,
(1)证明:
(2)计算 的值
的值
已知集合
(1)求 ;(2)求
;(2)求 ;(3)若
;(3)若 ,求a的取值范围。
,求a的取值范围。
已知点 ,圆
,圆 ,过点
,过点 的动直线
的动直线 与圆
与圆 交于
交于 两点,线段
两点,线段 的中点为
的中点为 ,O为坐标原点.
,O为坐标原点.
(1)求 的轨迹方程;
的轨迹方程;
(2)当 时,求
时,求 的方程及
的方程及 的面积.
的面积.
已知圆M:(x+1)2+y2=1,圆N:(x-1)2+y2=9,动圆P与圆M外切并且与圆N内切,圆心P的轨迹为曲线C.
(1)求C的方程;
(2)l是与圆P,圆M都相切的一条直线,l与曲线C交于A,B两点,当圆P的半径最长时,求|AB|.
设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A为C上一点,已知以F为圆心,FA为半径的圆F交l于B,D两点.
(1)若∠BFD=90°,△ABD的面积为 ,求p的值及圆F的方程;
,求p的值及圆F的方程;
(2)若A,B,F三点在同一直线m上,直线n与m平行,且n与C只有一个公共点,求坐标原点到m,n距离的比值.