延迟退休年龄的问题,近期引发社会的关注.人社部于2012年7月25日上午召开新闻发布会表示,我国延迟退休年龄将借鉴国外经验,拟对不同群体采取差别措施,并以“小步慢走”的方式实施.推迟退休年龄似乎是一种必然趋势,然而反对的声音也随之而起.现对某市工薪阶层关于“延迟退休年龄”的态度进行调查,随机抽取了50人,他们月收入的频数分布及对“延迟退休年龄”反对的人数
| 月收入(元) |
[1000,2000) |
[2000,3000) |
[3000,4000) |
[4000,5000) |
[5000,6000) |
[6000,7000) |
| 频数 |
5 |
10 |
15 |
10 |
5 |
5 |
| 反对人数 |
4 |
8 |
12 |
5 |
2 |
1 |
(1)由以上统计数据估算月收入高于4000的调查对象中,持反对态度的概率;
(2)若对月收入在[1000,2000),[4000,5000)的被调查对象中各随机选取两人进行跟踪调查,记选中的4人中赞成“延迟退休年龄”的人数为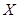 ,求
,求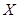 的分布列和数学期望.
的分布列和数学期望.
设 是锐角三角形,
是锐角三角形, 分别是内角A、B、C所对边长,并且
分别是内角A、B、C所对边长,并且 .
.
(1)求角 ;
;
(2)若 ,且
,且 ,求边
,求边 .
.
已知函数
(1)讨论函数 的单调性;
的单调性;
(2)若函数 的图象在点
的图象在点 处的切线的倾斜角为
处的切线的倾斜角为 ,对于任意的
,对于任意的 ,函数
,函数 在区间
在区间  上总不是单调函数,
上总不是单调函数,
求实数 的取值范围;
的取值范围;
(3)求证
已知两点 及
及 ,点
,点 在以
在以 、
、 为焦点的椭圆
为焦点的椭圆 上,且
上,且 、
、 、
、 构成等差数列.
构成等差数列.
(1)求椭圆 的方程;
的方程;
(2)如图,动直线 与椭圆
与椭圆 有且仅有一个公共点,点
有且仅有一个公共点,点 是直线上的两点,且
是直线上的两点,且 ,
, . 求四边形
. 求四边形 面积
面积 的最大值.
的最大值.
如图,已知多面体 中,
中,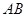 ⊥平面
⊥平面 ,
,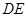 ⊥平面
⊥平面 ,
,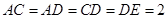 ,
, ,
, 为
为 的中点.
的中点.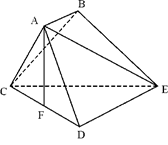
(1)求证: ⊥平面
⊥平面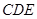 ;
;
(2)求二面角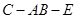 的大小.
的大小.
某集团公司举办一次募捐爱心演出,有1000人参加,每人一张门票,每张100元。在演出过程中穿插抽奖活动,第一轮抽奖从这1000张票根中随机抽取10张,其持有者获得价值1000元的奖品,并参加第二轮抽奖活动。第二轮抽奖由第一轮获奖者独立操作按钮,电脑随机产生两个数 (
(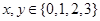 ),满足
),满足 电脑显示“中奖”,且抽奖者获得特等奖奖金;否则电脑显示“谢谢”,则不中奖。
电脑显示“中奖”,且抽奖者获得特等奖奖金;否则电脑显示“谢谢”,则不中奖。
(1)已知小明在第一轮抽奖中被抽中,求小明在第二轮抽奖中获奖的概率;
(2)若该集团公司望在此次活动中至少获得61875元的收益,则特等奖奖金最高可设置成多少元?