某集团公司举办一次募捐爱心演出,有1000人参加,每人一张门票,每张100元。在演出过程中穿插抽奖活动,第一轮抽奖从这1000张票根中随机抽取10张,其持有者获得价值1000元的奖品,并参加第二轮抽奖活动。第二轮抽奖由第一轮获奖者独立操作按钮,电脑随机产生两个数 (
(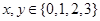 ),满足
),满足 电脑显示“中奖”,且抽奖者获得特等奖奖金;否则电脑显示“谢谢”,则不中奖。
电脑显示“中奖”,且抽奖者获得特等奖奖金;否则电脑显示“谢谢”,则不中奖。
(1)已知小明在第一轮抽奖中被抽中,求小明在第二轮抽奖中获奖的概率;
(2)若该集团公司望在此次活动中至少获得61875元的收益,则特等奖奖金最高可设置成多少元?
已知数列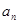 满足
满足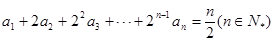
(Ⅰ)求数列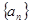 的通项;
的通项;
(Ⅱ)若 求数列
求数列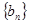 的前n项
的前n项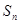 和
和
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上D点在AN上,且对角线MN过点C,已知AB=3米,AD=2米。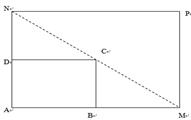
(Ⅰ)要使矩形AMPN的面积大于32平方米,则DN的长应在什么范围内?
(Ⅱ)当DN 的长度为多少时,矩形花坛AMPN的面积最小?并求出最小值。
已知函数 是定义在R上的单调函数,满足
是定义在R上的单调函数,满足 ,且对任意的实数
,且对任意的实数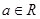 有
有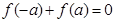 恒成立
恒成立
(Ⅰ)试判断 在R上的单调性,并说明理由.
在R上的单调性,并说明理由.
(Ⅱ)解关于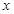 的不等式
的不等式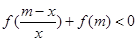 ,其中
,其中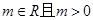
.已知函数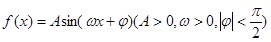 的图像与y轴的交点为
的图像与y轴的交点为 他在y轴右侧的第一个最高点和第一个最低点的坐标分别为
他在y轴右侧的第一个最高点和第一个最低点的坐标分别为 和
和 。
。
(Ⅰ)求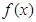 的解析式及
的解析式及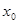 值;
值;
(Ⅱ)若锐角 满足
满足 ,求
,求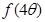 的值
的值
14分)已知函数
(1)当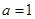 时,求函数
时,求函数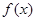 的最值;
的最值;
(2)求函数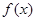 的
的 单调
单调 区间;
区间;
(3)说明是否存在实数 使
使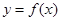 的图象与
的图象与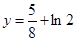 无公共点.
无公共点.