14分)已知函数
(1)当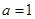 时,求函数
时,求函数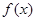 的最值;
的最值;
(2)求函数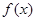 的
的 单调
单调 区间;
区间;
(3)说明是否存在实数 使
使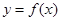 的图象与
的图象与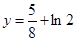 无公共点.
无公共点.
在△ABC中,角A,B,C所对的边分别为a,b,c,且
(I)求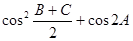 的值;
的值;
(II)若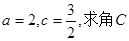 的大小。
的大小。
(本大题10分)
设函数 ,
, ,且
,且 ;
;
(1)求 ;
;
(2)若当 时,
时,
 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
(本大题8分)在 中,
中, 分别是角
分别是角 的对边,
的对边, 为
为 的面积,若
的面积,若 ,且
,且
(1).求 的值;(2).求
的值;(2).求 的最大值。
的最大值。
(本大题8分)已知函数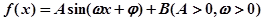 的一系列对应值如下表:
的一系列对应值如下表:
| x |
 |
 |
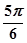 |
 |
 |
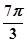 |
 |
| y |
-1 |
1 |
3 |
1 |
-1 |
1 |
3 |
(1).根据表格提供的数据,求函数的一个解析式;
(2).根据(1)的结果,若函数 的周期为
的周期为 ,当
,当 时,方程
时,方程 恰有两个不同的解,求m的取值范围。
恰有两个不同的解,求m的取值范围。
(本大题8分)定义运算 ,若函数
,若函数
 ,当
,当 时,
时,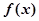 的最大值与最小值的和为2.
的最大值与最小值的和为2.
(1).求 的值,并用五点法画出
的值,并用五点法画出 在长度为一个周期的区间内的简图。
在长度为一个周期的区间内的简图。
(2).求函数 的单调区间。
的单调区间。