已知函数 .
.
(1)求函数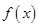 在
在 上的最小值;
上的最小值;
(2)若函数 有两个不同的极值点
有两个不同的极值点 、
、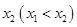 且
且 ,求实数
,求实数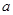 的取值范围.
的取值范围.
设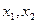 是函数
是函数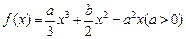 的两个极值点,且
的两个极值点,且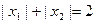
(Ⅰ)求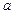 的取值范围;
的取值范围;
(Ⅱ)求证: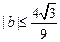 .
.
已知函数f(x)=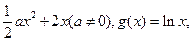
(1)若h(x)=f(x)-g(x)存在单调增区间,求a的取值范围;
(2)是否存在实数a>0,使得方程 在区间
在区间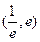 内有且只有两个不相等的实数根?若存在,求出a的取值范围?若不存在,请说明理由。
内有且只有两个不相等的实数根?若存在,求出a的取值范围?若不存在,请说明理由。
已知函数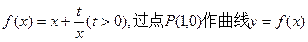 的两条切线PM、PN,切点分别为M、N.
的两条切线PM、PN,切点分别为M、N.
(I)当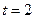 时,求函数
时,求函数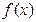 的单调递增区间;
的单调递增区间;
(II)设|MN|=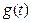 ,试求函数
,试求函数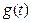 的表达式;
的表达式;
(III)在(II)的条件下,若对任意的正整数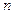 ,在区间
,在区间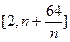 内,总存在m+1个数
内,总存在m+1个数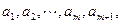 使得不等式
使得不等式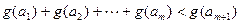 成立,求m的最大值.
成立,求m的最大值.
设曲线 处的切线l与x轴、y轴所围成的三角形面积为S(t).
处的切线l与x轴、y轴所围成的三角形面积为S(t).
(Ⅰ)求切线l的方程;
(Ⅱ)求S(t)的最大值.
已知函数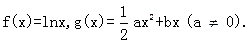
(I)若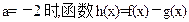 在其定义域是增函数,求b的取值范围;
在其定义域是增函数,求b的取值范围;
(II)在(I)的结论下,设函数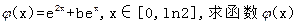 的最小值;
的最小值;
(III)设函数 的图象C1与函数
的图象C1与函数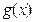 的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.