设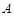 是由
是由 个实数组成的
个实数组成的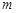 行
行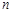 列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
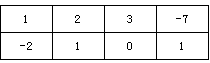
(1)数表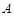 如表1所示,若经过两“操”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);表1
如表1所示,若经过两“操”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);表1
| 1 |
2 |
3 |
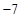 |
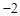 |
1 |
0 |
1 |
(2)数表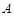 如表2所示,若必须经过两次“操作”,才可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数
如表2所示,若必须经过两次“操作”,才可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数 的所有可能值;表2
的所有可能值;表2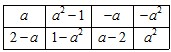
(3)对由 个实数组成的
个实数组成的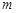 行
行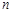 列的任意一个数表
列的任意一个数表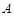 ,能否经过有限次“操作”以后,使得到的数表每行的各数之和与每列的各数之和均为非负实数?请说明理由.
,能否经过有限次“操作”以后,使得到的数表每行的各数之和与每列的各数之和均为非负实数?请说明理由.
(本小题满分10分)已知直三棱柱 中,
中, ,
, 是棱
是棱 的中点.如图所示.
的中点.如图所示.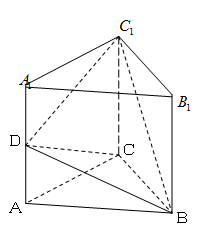
(1)求证: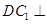 平面
平面 ;
;
(2)求锐二面角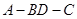 的大小.
的大小.
(本小题满分10分)已知圆C的极坐标方程为 =2,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,若直线
=2,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,若直线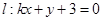 与圆C相切.
与圆C相切.
求(1)圆C的直角坐标方程;
(2)实数k的值.
(本小题满分10分)已知函数f(x)=ln(2x-e), 点P(e,f(e))为函数的图像上一点
(1)求导函数 的解析式;
的解析式;
(2)求f(x)=ln(2x-e)在点P(e,f(e))处的切线的方程.
(本小题满分16分)设函数f(x)=xsinx(x∈R),
(Ⅰ)证明f(x+2kπ)-f(x)=2kπsinx,其中k为整数;
(Ⅱ)设x0为f(x)的一个极值点,证明  ;
;
(提示 )
)
(Ⅲ)设f(x)在(0,+∞)内的全部极值点按从小到大的顺序排列a1,a2, ,an, ,证明 .
.
(本小题满分16分)已知函数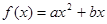 的图像过点
的图像过点 ,且在
,且在 处的切线的斜率为
处的切线的斜率为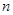 ,(
,(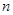 为正整数)
为正整数)
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)若数列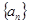 满足:
满足: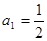 ,
, ,令
,令 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅲ)对于(Ⅱ)中的数列 ,令
,令 ,求数列
,求数列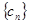 的前
的前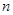 项的和
项的和 .
.