电子所带电荷量最早是由美国科学家密立根所做的油滴实验测得的。密立根油滴实验的原理如图所示:两块水平放置的平行金属板与电源相连接,上板带正电,下板带负电,油滴从喷雾器喷出后,由于与喷嘴摩擦而带负电,油滴散布在油滴室中,在重力作用下,少数油滴通过上面金属板的小孔进入(可认为初速度为0)平行金属板间,落到两板之间的匀强电场中。在强光照射下,观察者通过显微镜观察油滴的运动。
从喷雾喷出的小油滴可以视为球形,小油滴在空气中下落时受到的空气阻力f大小跟它下落的速度v的大小的关系是:f=6πηrv,式中r为油滴半径,η为粘滞系数。设重力加速度为g,不考虑油滴的蒸发。
(1)实验中先将开关断开,测出小油滴下落一段时间后达到匀速运动时的速度v1,已知油的密度为ρ,空气的密度为ρ′,粘滞系数为η,试由以上数据计算小油滴的半径r;
(2)待小球向下运动的速度达到v1后,将开关闭合,小油滴受电场力作用,最终达到向上匀速运动,测得匀速运动的速度v2,已知两金属板间的距离为d,电压为U。试由以上数据计算小油滴所带的电荷量q;
(3)大致(不要求精确的标度)画出油滴从进入平行金属板到向上匀速运动这段过程中的v—t图像(设竖直向下为正方向)。
如图,一定质量的理想气体被不计质量的活塞封闭在可导热的气缸内,活塞距底部的高度为h,可沿气缸无摩擦地滑动。取一小盒沙子缓慢地倒在活塞的上表面上,沙子倒完时,活塞下降了h/5。再取相同质量的一小盒沙子缓慢地倒在活塞的上表面上。外界大气的压强和温度始终保持不变,已知大气压为p0,活塞横截面积为S,重力加速度为g,求:
(1)一小盒沙子的质量;
(2)沙子再次倒完时活塞距气缸底部的高度。
如图线圈的面积是0.05 m2,共100匝,线圈电阻为r =" 1" Ω,外接电阻R =" 9" Ω,匀强磁场的磁感应强度B = T,当线圈以300 r/min的转速匀速旋转时,求:(此题最后结果可保留根号)
T,当线圈以300 r/min的转速匀速旋转时,求:(此题最后结果可保留根号)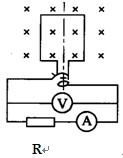
(1)若线圈从图示位置开始计时,写出线圈中感应电动势瞬时值表达式.
(2)电路中电压表和电流表的示数各是多少?
(3)由图示位置转过90°角的过程中,电阻R上产生的热量为多少?
(4)由图示位置转过180°角的过程中,流经电阻R上的电量为多少?
图为一理想变压器,ab为原线圈,ce为副线圈,d为副线圈引出的一个接头。原线圈输入正弦式交变电压的u-t图象如右图所示。若只在ce间接一只Rce="400" Ω的电阻,或只在de间接一只Rde="225" Ω的电阻,两种情况下电阻消耗的功率均为80W。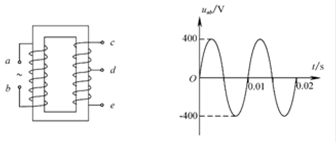
(1)求只在ce间接400Ω的电阻时,原线圈中的电流I1;
(2)求ce和de 间线圈的匝数比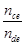 。
。
已知铜的摩尔质量M =6.4×10-2 kg/mol,铜的密度  =8.9×103kg/m3,阿伏加德罗常数NA=6.0×1023mol-1.试估算:(计算结果保留2位有效数字)
=8.9×103kg/m3,阿伏加德罗常数NA=6.0×1023mol-1.试估算:(计算结果保留2位有效数字)
⑴一个铜原子的质量.
⑵若每个铜原子可提供两个自由电子,则3.0×10-5m3的铜导体中有多少个自由电子?
如图所示,正方形导线框ABCD每边长L=0.2m,线框电阻R=0.1Ω,质量m=0.1kg。物体M的质量为0.3kg。匀强有界磁场高也为L=0.2m,B=0.5T。物体M放在光滑斜面上,斜面倾角为30°。物体从静止开始下滑,当线框AD边进入磁场时,恰好开始做匀速运动。求:(g取10m/s2)
(1)线框做匀速运动的速度大小;
(2)线框做匀速运动过程中,物体M对线框做的功;
(3)线框做匀速运动过程中,若与外界无热交换,线框内能的增量。