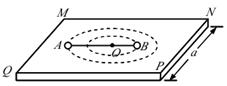
如下图1所示，水平面内的直角坐标系的第一象限有磁场分布，方向垂直于水平面向下，磁感应强度沿y轴方向没有变化，与横坐标x的关系如下图2所示，图线是双曲线（坐标轴是渐进线）；顶角θ=45°的光滑金属长导轨 MON固定在水平面内，ON与x轴重合，一根与ON垂直的长导体棒在水平向右的外力作用下沿导轨MON向右滑动，导体棒在滑动过程中始终保持与导轨良好接触。已知t=0时，导体棒位于顶角O处；导体棒的质量为m=2kg；OM、ON接触处O点的接触电阻为R=0.5Ω，其余电阻不计；回路电动势E与时间t的关系如图3所示，图线是过原点的直线。求：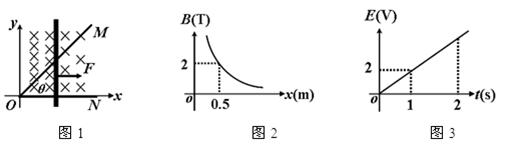
（1）t=2s时流过导体棒的电流强度I2的大小；
（2）1～2s时间内回路中流过的电量q的大小；
（3）导体棒滑动过程中水平外力F（单位：N）与横坐标x（单位：m）的关系式。
如图所示，AOB是1/4圆柱玻璃砖的截面，玻璃砖的折射率为
。一束平行光以45°入射角射向玻璃砖的OA平面，这些光线中只有一部分能从圆柱的AB面上射出。假设凡射到OB面的光线全部被吸收，也不考虑OA面的反射作用，试求圆柱AB面上能射出光线的部分占AB表面的几分之几?
如图所示，固定的绝热气缸内有一质量为m的“T”型绝热活塞（体积可忽略），距气缸底部h0处连接一U形管（管内气体的体积忽略不计）。初始时，封闭气体温度为T0，活塞距离气缸底部为1.5h0，两边水银柱存在高度差。已知水银的密度为ρ，大气压强为p0，气缸横截面积为S，活塞竖直部分长为1.2h0，重力加速度为g。求：
①初始时，水银柱两液面高度差。
②通过制冷装置缓慢降低气体温度，当温度为多少时两水银面相平。
如图所示，在xoy平面直角坐标系第一象限内分布有垂直向外的匀强磁场，磁感应强度大小B=2.5×10-2T，在第二象限紧贴y轴和x轴放置一对平行金属板MN（中心轴线过y轴），极板间距d=0.4m，极板与左侧电路相连接。通过移动滑动头P可以改变极板MN间的电压。a、b为滑动变阻器的最下端和最上端（滑动变阻器的阻值分布均匀），a、b两端所加电压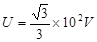
。在MN中心轴线上距y轴距离为L=0.4m处有一粒子源S，沿x轴正方向连续射出比荷为
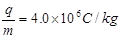，速度为vo=2.0×104m/s带正电的粒子，粒子经过y轴进入磁场后从x轴射出磁场（忽略粒子的重力和粒子之间的相互作用）。
（1）当滑动头P在ab正中间时，求粒子射入磁场时速度的大小。
（2）当滑动头P在ab间某位置时，粒子射出极板的速度偏转角为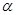
，试写出粒子在磁场中运动的时间与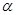的函数关系，并由此计算粒子在磁场中运动的最长时间。
两个完全相同的物块A、B，质量均为m="0.8" kg，沿同一粗糙水平面以相同的初速度从同一位置运动。利用速度传感器可以在计算机上得到它们速度随时间的变化关系如图所示，图中的两条直线分别表示A物块受到水平拉力F作用和B物块不受拉力作用的v-t图象。求：
（1）物块A所受拉力F的大小。
（2）4 s末物块A、B之间的距离s。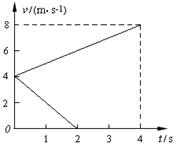
如图所示，一水平光滑、距地面高为 h、边长为 a 的正方形 MNPQ 桌面上，用长为 L 的不可伸长的轻绳连接质量分别为mA、mB的 A、B 两小球．两小球在绳子拉力的作用下，绕绳子上的某点 O 以不同的线速度做匀速圆周运动，圆心 O 与桌面中心重合．已知 mA 0.5kg，L1.2m，LAO 0.8m，a2.1m，h 1.25m，A 球的速度大小v A 0.4m/s，重力加速度 g 取 10m/s2，求：
（1）绳子上的拉力 F 以及 B 球的质量m B；
（2）若当绳子与 MN 平行时突然断开，则经过 1.5s两球的距离；
（3）两小球落至地面时，落点的距离．