如图，在四棱锥
中，平面
平面
，
，
是等边三角形，已知
.
（1）设
是
上的一点，证明：平面平面
；
（2）求二面角
的余弦值.
设定函数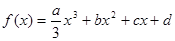
(
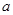＞0)，且方程
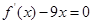的两个根分别为1，4。
（Ⅰ）当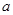=3且曲线
过原点时，求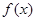
的解析式；
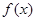（Ⅱ）若在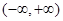
无极值点，求a的取值范围。
已知命题
若非
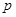是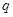
的充分不必要条件，求
的取值范围.
已知函数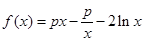
.
（1）若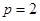
，求曲线
在点
处的切线方程；
（2）若函数在其定义域内为增函数，求正实数
的取值范围；
（3）设函数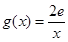
，若在
上至少存在一点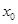
，使得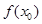
＞
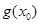成立，求实数的取值范围。
设
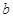和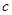
分别是先后抛掷一枚骰子得到的点数，用随机变量
表示方程
实根的个数（重根按一个计）．
（1）求方程有实根的概率；
（2）求的分布列和数学期望；
（3）求在先后两次出现的点数中有5的条件下，方程有实根的概率.
已知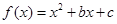
为偶函数，曲线
过点（2,5）,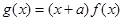 
.
（1）若曲线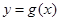
有斜率为0的切线，求实数
的取值范围；
（2）若当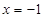
时函数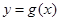取得极值，确定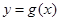的单调区间.