某高校在2013年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组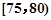 ,第2组
,第2组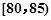 ,第3组
,第3组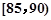 ,第4组
,第4组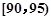 ,第5组
,第5组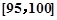 ,得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
,得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
(Ⅰ)求出第4组的频率,并补全频率分布直方图;
(Ⅱ)根据样本频率分布直方图估计样本的中位数;
(Ⅲ)如果用分层抽样的方法从“优秀”和“良好” 的学生中共选出5人,再从这5人中选2人,那么至少有一人是“优秀”的概率是多少?
已知 ,
,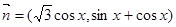 ,函数
,函数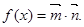
(1)求函数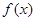 的解析式;
的解析式;
(2)在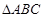 中,角
中,角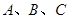 的对边为
的对边为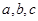 ,若
,若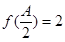 ,
,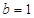 ,
,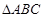 的面积为
的面积为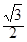 ,求a的值.
,求a的值.
已知椭圆C: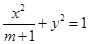 的两个焦点是F1(
的两个焦点是F1(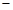 c,0),F2(c,0)(c>0)。
c,0),F2(c,0)(c>0)。
(I)若直线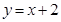 与椭圆C有公共点,求
与椭圆C有公共点,求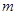 的取值范围;
的取值范围;
(II)设E是(I)中直线与椭圆的一个公共点,求|EF1|+|EF2|取得最小值时,椭圆的方程;
(III)已知斜率为k(k≠0)的直线l与(II)中椭圆交于不同的两点A,B,点Q满足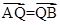 且
且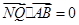 ,其中N为椭圆的下顶点,求直线l在y轴上截距的取值范围.
,其中N为椭圆的下顶点,求直线l在y轴上截距的取值范围.
已知函数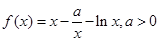 .
.
(I)讨论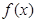 的单调性;
的单调性;
(Ⅱ)若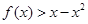 在(1,+
在(1,+ )恒成立,求实数a的取值范围.
)恒成立,求实数a的取值范围.
已知等差数列{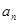 }的首项a1=1,公差d>0,且
}的首项a1=1,公差d>0,且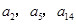 分别是等比数列{
分别是等比数列{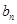 }的b2,b3,b4.
}的b2,b3,b4.
(I)求数列{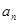 }与{{
}与{{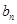 }的通项公式;
}的通项公式;
(Ⅱ)设数列{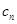 }对任意自然数n均有
}对任意自然数n均有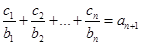 成立,求
成立,求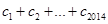 的值.
的值.
某中学经市批准建设分校,工程从2010年底开工到2013年底完工,分三期完成,经过初步招标淘汰后,确定由甲、乙两建筑公司承建,且每期工程由两公司之一独立完成,必须在建完前一期工程后再建后一期工程,已知甲公司获得第一期,第二期,第三期工程承包权的概率分别是 ,
, ,
, .
.
(I)求甲乙两公司均至少获得l期工程的概率;
(II)求甲公司获得的工程期数的分布列和数学期望E(X).