已知函数 .
.
(I)求f(x)的单调区间及极值;
(II)若关于x的不等式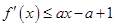 恒成立,求实数a的集合.
恒成立,求实数a的集合.
以下是某地搜集到的新房屋的销售价格y和房屋的面积x的数据:
| 房屋面积x(m2) |
115 |
110 |
80 |
135 |
105 |
| 销售价格y(万元) |
24.8 |
21.6 |
18.4 |
29.2 |
22 |
(1)画出数据对应的散点图;
(2)求线性回归方程,并在散点图中加上回归直线.
在研究硝酸钠的可溶性程度时,对于不同的温度观测它在水中的溶解度,得观测结果如下:
| 温度(x) |
0 |
10 |
20 |
50 |
70 |
| 溶解度(y) |
66.7 |
76.0 |
85.0 |
112.3 |
128.0 |
由资料看y与x呈线性相关,试求回归方程.
为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小长方形面积之比为2∶4∶17∶15∶9∶3,第二小组频数为12.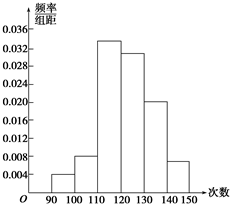
(1)第二小组的频率是多少?样本容量是多少?
(2)若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少?
(3)在这次测试中,学生跳绳次数的中位数落在哪个小组内?请说明理由.
在育民中学举行的电脑知识竞赛中,将九年级两个班参赛的学生成绩(得分均为整数)进行整理后分成五组,绘制如图所示的频率分布直方图.已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.30,0.15,0.10,0.05,第二小组的频数是40.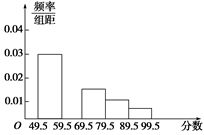
(1)求第二小组的频率,并补全这个频率分布直方图;
(2)求这两个班参赛的学生人数是多少?
(3)这两个班参赛学生的成绩的中位数应落在第几小组内?(不必说明理由)
有甲、乙两位射击运动员在相同条件下各射击10次,记录各次命中环数;
甲:8,8,6,8,6,5,9,10,7,4
乙:9,5,7,8,7,6,8,6, 8,7
(1)分别计算他们环数的标准差;
(2)谁的射击情况比较稳定.