如图所示,在直三棱柱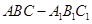 中,
中, ,
, 为
为 的中点.
的中点.
(Ⅰ) 若AC1⊥平面A1BD,求证:B1C1⊥平面ABB1A1;
(Ⅱ)在(Ⅰ)的条件下,设AB=1,求三棱锥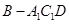 的体积.
的体积.
数列{an}中,a1=8,a4=2且满足an+2=2an+1-an n∈N
(1)求数列{an}的通项公式;
(2)设Sn=|a1|+|a2|+…+|an|,求sn;
(3)设bn=( n∈N),Tn=b1+b2+…+bn( n∈N),是否存在最大的整数m,使得对任意n∈N,均有Tn>成立?若存在,求出m的值;若不存在,请说明理由。
已知等差数列{an}中,a2=8,前10项和S10=185.
(1)求通项an;
(2)若从数列{an}中依次取第2项、第4项、第8项…第2n项……按原来的顺序组成一个新的数列{bn},求数列{bn}的前n项和Tn.
已知等差数列{an}中,a2=8,前10项和S10=185.
(1)求通项an;
(2)若从数列{an}中依次取第2项、第4项、第8项…第2n项……按原来的顺序组成一个新的数列{bn},求数列{bn}的前n项和Tn.
数列{an}中,a1=8,a4=2且满足an+2=2an+1-an n∈N
(1)求数列{an}的通项公式;
(2)设Sn=|a1|+|a2|+…+|an|,求sn;
(3)设bn=( n∈N),Tn=b1+b2+…+bn( n∈N),是否存在最大的整数m,使得对任意n∈N,均有Tn>成立?若存在,求出m的值;若不存在,请说明理由。
在数列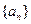 中,
中,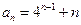 ,
,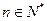 .
.
(1)求数列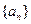 的前
的前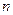 项和
项和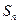 ;(2)证明不等式
;(2)证明不等式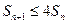 ,对任意
,对任意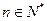 皆成立。
皆成立。