(本题12分)在如图所示的四面体ABCD中,AB、BC、CD两两互相垂直,且BC=CD=1。(1)求证:平面ACD⊥平面ABC;(2)求二面角C-AB-D的大小。

(本题12分)已知命题p:|4-x|≤6,q:x2-2x+1- a2≥0(a>0),若非p是q的充分不必要条件,求a的取值范围。
(本题12分)在锐角△ABC中,a,b,c分别为角A、B、C所对的边,且 a=2csinA,(1)确定角C的大小;(2)若c=
a=2csinA,(1)确定角C的大小;(2)若c= ,且△ABC的面积为
,且△ABC的面积为 ,求a+b的值。
,求a+b的值。
如图,四边形ABCD是一个边长为100米的正方形地皮,其中ATPS是一半径为90米的扇形小山,其余部分都是平地,P是弧TS上一点,现有一位开发商想在平地上建造一个两边落在BC与CD上的长方形停车场PQCR.
|
已知b>-1,c>0,函数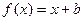 的图象与函数
的图象与函数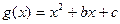 的图象相切.
的图象相切.
(Ⅰ)设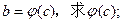
(Ⅱ)是否存在常数c,使得函数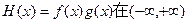 内有极值点?若存在,求出c的取值范围;若不存在,请说明理由.
内有极值点?若存在,求出c的取值范围;若不存在,请说明理由.