如图,四边形ABCD是一个边长为100米的正方形地皮,其中ATPS是一半径为90米的扇形小山,其余部分都是平地,P是弧TS上一点,现有一位开发商想在平地上建造一个两边落在BC与CD上的长方形停车场PQCR.
|
已知在直角坐标系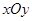 中,直线
中,直线 的参数方程为
的参数方程为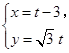 (
(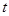 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系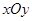 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以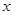 轴正半轴为极轴)中,曲线
轴正半轴为极轴)中,曲线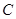 的极坐标方程为
的极坐标方程为 .
.
①求直线 普通方程和曲线
普通方程和曲线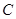 的直角坐标方程;
的直角坐标方程;
②设点 是曲线
是曲线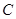 上的一个动点,求它到直线
上的一个动点,求它到直线 的距离的取值范围.
的距离的取值范围.
已知矩阵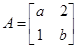 有一个属于特征值
有一个属于特征值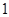 的特征向量
的特征向量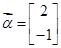 ,
,
①求矩阵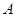 ;
;
②已知矩阵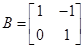 ,点
,点 ,
,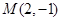 ,
, ,求
,求 在矩阵
在矩阵 的对应变换作用下所得到的
的对应变换作用下所得到的 的面积.
的面积.
己知函数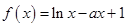 在
在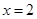 处的切线斜率为
处的切线斜率为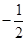 .
.
(1)求实数 的值及函数
的值及函数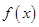 的单调区间;
的单调区间;
(2)设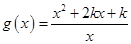 ,对
,对 使得
使得 恒成立,求正实数
恒成立,求正实数 的取值范围;
的取值范围;
(3)证明: .
.
函数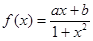 是定义在
是定义在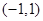 上的奇函数,且
上的奇函数,且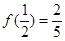 .
.
(1)求函数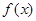 的解析式;
的解析式;
(2)证明函数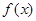 在
在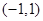 上是增函数;
上是增函数;
(3)解不等式: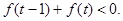 .
.
已知函数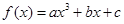 在
在 处取得极值为
处取得极值为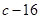
(1)求
 的值;(2)若
的值;(2)若 有极大值28,求
有极大值28,求 在
在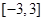 上的最小值.
上的最小值.