已知矩阵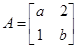 有一个属于特征值
有一个属于特征值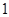 的特征向量
的特征向量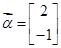 ,
,
①求矩阵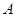 ;
;
②已知矩阵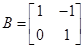 ,点
,点 ,
,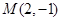 ,
, ,求
,求 在矩阵
在矩阵 的对应变换作用下所得到的
的对应变换作用下所得到的 的面积.
的面积.
(本小题满分14分)如图,在直线 之间表示的是一条河流,河流的一侧河岸(x轴)是一条公路,且公路随时随处都有公交车来往. 家住A(0,a)的某学生在位于公路上B(d,0)(d>0)处的学校就读. 每天早晨该学生都要从家出发,可以先乘船渡河到达公路上某一点,再乘公交车去学校,或者直接乘船渡河到达公路上B(d, 0)处的学校. 已知船速为
之间表示的是一条河流,河流的一侧河岸(x轴)是一条公路,且公路随时随处都有公交车来往. 家住A(0,a)的某学生在位于公路上B(d,0)(d>0)处的学校就读. 每天早晨该学生都要从家出发,可以先乘船渡河到达公路上某一点,再乘公交车去学校,或者直接乘船渡河到达公路上B(d, 0)处的学校. 已知船速为 ,车速为
,车速为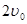 (水流速度忽略不计).
(水流速度忽略不计).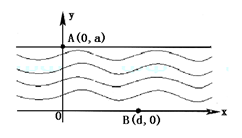
(1)若d=2a,求该学生早晨上学时,从家出发到达学校所用的最短时间;
(2)若 ,求该学生早晨上学时,从家出发到达学校所用的最短时间.
,求该学生早晨上学时,从家出发到达学校所用的最短时间.
(本小题满分14分)
已知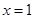 是函数
是函数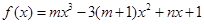 的一个极值点,其中
的一个极值点,其中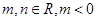 ,
,
(1)求 与
与 的关系式;
的关系式;
(2)求 的单调区间;
的单调区间;
(3)当 时,函数
时,函数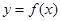 的图象上任意一点的切线斜率恒大于3
的图象上任意一点的切线斜率恒大于3 ,求
,求 的取值范围.
的取值范围.
(本小题满分14分)

(本小题满分12分)已知函数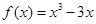
(1)求函数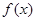 在
在 上的最大值和最小值.
上的最大值和最小值.
(2)过点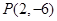 作曲线
作曲线 的切线,求此切线的方程.
的切线,求此切线的方程.
(本小题满分12分)求抛物线 与直线
与直线 围成的平面图形的面积.
围成的平面图形的面积.