已知函数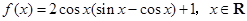 .
.
(1)求函数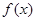 的单调递增取区间;
的单调递增取区间;
(2)将函数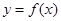 的图象向左平移
的图象向左平移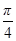 个单位后,再将图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数
个单位后,再将图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数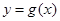 的图象,求
的图象,求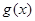 的最大值及取得最大值时的
的最大值及取得最大值时的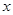 的集合.
的集合.
已知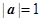 ,
,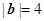 ,且向量
,且向量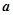 与
与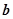 不共线.
不共线.
(1)若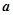 与
与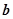 的夹角为
的夹角为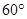 ,求
,求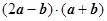 ;
;
(2)若向量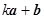 与
与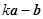 互相垂直,求
互相垂直,求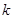 的值.
的值.
已知角 终边上一点P(-4,3),求
终边上一点P(-4,3),求 的值
的值
已知数列 满足
满足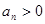 且对一切
且对一切 ,
,
有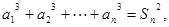
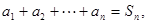
(Ⅰ)求证:对一切
(Ⅱ)求数列 通项公式.
通项公式.
(Ⅲ)求证:
已知椭圆
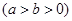 的离心率为
的离心率为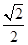 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线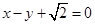 相切.
相切.
(I)求椭圆 的方程;
的方程;
(II)若过点 (2,0)的直线与椭圆
(2,0)的直线与椭圆 相交于两点
相交于两点 ,设
,设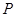 为椭圆上一点,且满足
为椭圆上一点,且满足 (O为坐标原点),当
(O为坐标原点),当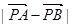 <
<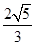 时,求实数
时,求实数 的取值范围.
的取值范围.