（本小题满分14分）在中学生综合素质评价某个维度的测评中，分“优秀、合格、尚待改进”三个等级进行学生互评．某校高一年级有男生500人，女生400人，为了了解性别对该维度测评结果的影响，采用分层抽样方法从高一年级抽取了45名学生的测评结果，并作出频数统计表如下：
（1）从表二的非优秀学生中随机选取2人交谈，求所选2人中恰有1人测评等级为合格的概率；
（2）由表中统计数据填写下边
列联表，并判断是否有
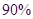的把握认为“测评结果优秀与性别有关”．
| |
男生 |
女生 |
总计 |
| 优秀 |
|
|
|
| 非优秀 |
|
|
|
| 总计 |
|
|
|
参考数据与公式：
，其中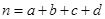
．
临界值表：
 |
 |
|
 |
 |
 |
 |
 |
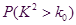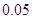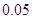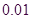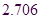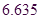如图，四棱锥P－ABCD的底面ABCD为矩形，且PA="AD=1,AB=2,"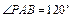 
,
.
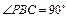(1)求证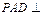：平面
平面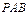
；
(2)求三棱锥D－PAC的体积；
(3)求直线PC与平面ABCD所成角的正弦值．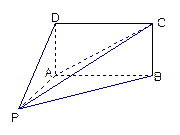
锐角三角形ABC的三内角A、B、C所对边的长分别为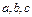
，设向量
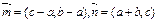，且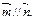
（1）求角B的大小；
（2）若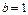
，求
的取值范围。
已知：向量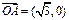
，O为坐标原点，动点M满足：
.
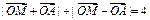(1)求动点 M的轨迹 C的方程；
（2）已知直线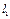
、
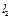都过点
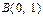，且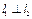
，
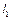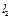、与轨迹C分别交于点D、E.是否存在这样的直线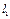、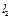,使得△BDE是等腰直角三角形?若存在，指出这样的直线共有几组(无需求出直线的方程)；若不存在，请说明理由.
设数列
的前n项和为Sn，满足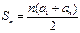
，数列
满足
.
（1）求证：数列为等差数列；
（2）若
，求数列与的通项公式；
（3）在（2）的条件下，设数列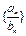
的前n项和Tn，试比较
与
的大小.
某校教务处要对高三上学期期中数学试卷进行调研，考察试卷中某道填空题的得分情况.已知该题有两空，第一空答对得3分，答错或不答得0分；第二空答对得2分，答错或不答得0分.第一空答对与否与第二空答对与否是相互独立的.从该校1468份试卷中随机抽取1000份试卷，其中该题的得分组成容量为1000的样本，统计结果如下表：
| 第一空得分情况 |
第二空得分情况 |
|||||
| 得分 |
0 |
3 |
得分 |
0 |
2 |
|
| 人数 |
198 |
802 |
人数 |
698 |
302 |
（Ⅰ）求样本试卷中该题的平均分，并据此估计该校高三学生该题的平均分.
（Ⅱ）该校的一名高三学生因故未参加考试，如果这名学生参加考试，以样本中各种得分情况的频率（精确到0.1）作为该同学相应的各种得分情况的概率.试求该同学这道题得分
的数学期望.