某校教务处要对高三上学期期中数学试卷进行调研,考察试卷中某道填空题的得分情况.已知该题有两空,第一空答对得3分,答错或不答得0分;第二空答对得2分,答错或不答得0分.第一空答对与否与第二空答对与否是相互独立的.从该校1468份试卷中随机抽取1000份试卷,其中该题的得分组成容量为1000的样本,统计结果如下表:
| 第一空得分情况 |
|
第二空得分情况 |
||||
| 得分 |
0 |
3 |
|
得分 |
0 |
2 |
| 人数 |
198 |
802 |
|
人数 |
698 |
302 |
(Ⅰ)求样本试卷中该题的平均分,并据此估计该校高三学生该题的平均分.
(Ⅱ)该校的一名高三学生因故未参加考试,如果这名学生参加考试,以样本中各种得分情况的频率(精确到0.1)作为该同学相应的各种得分情况的概率.试求该同学这道题得分 的数学期望.
的数学期望.
已知数列 中
中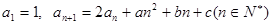 .
.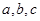 为实常数.
为实常数.
(Ⅰ)若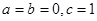 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅱ)若 .①是否存在常数
.①是否存在常数 求出
求出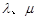 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
②设  .证明:n≥2时,
.证明:n≥2时, .
.
已知函数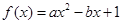 .
.
(Ⅰ)若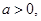 不等式
不等式 的解集为
的解集为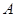 ,
,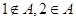 ,求
,求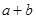 的取值范围;
的取值范围;
(Ⅱ)若 为整数,
为整数, ,且函数
,且函数 在
在 上恰有一个零点,求
上恰有一个零点,求 的值;
的值;
(Ⅲ)在(Ⅱ)的条件下,若函数 对任意的x∈
对任意的x∈ ,有
,有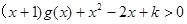 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.
甲方是一农场,乙方是一工厂,由于乙方生产须占用甲方的资源,因此甲方每年向乙方索赔以弥补经济损失并获得一定净收入.乙方在不赔付甲方的情况下,乙方的年利润 (元)与年产量
(元)与年产量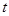 (吨)满足函数关系
(吨)满足函数关系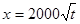 .若乙方每生产一吨产品必须赔付甲方
.若乙方每生产一吨产品必须赔付甲方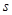 元(以下称
元(以下称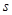 为赔付价格).
为赔付价格).
(Ⅰ)将乙方的年利润w (元)表示为年产量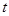 (吨)的函数,并求出乙方获得最大利润的年产量;
(吨)的函数,并求出乙方获得最大利润的年产量;
(Ⅱ)甲方每年受乙方生产影响的经济损失金额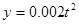 (元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格
(元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格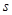 是多少?
是多少?
已知圆 :
: .
.
(Ⅰ)直线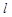 过点
过点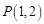 ,且与圆
,且与圆 交于
交于 、
、 两点,若
两点,若 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)过圆 上一动点
上一动点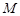 作平行于
作平行于 轴的直线
轴的直线 ,设
,设 与
与 轴的交点为
轴的交点为 ,若向量
,若向量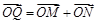 ,求动点
,求动点 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
设函数f(x)=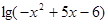 的定义域为A,函数g(x)=
的定义域为A,函数g(x)=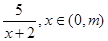 的值域为B.
的值域为B.
(Ⅰ)当m=2时,求A∩B;
(Ⅱ)若“x∈A”是“x∈B”的必要不充分条件,求实数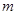 的取值范围.
的取值范围.