已知椭圆 的离心率为
的离心率为 ,其左右焦点分别为
,其左右焦点分别为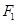 、
、 ,
, ,设点
,设点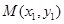 ,
,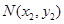 是椭圆上不同两点,且这两点与坐标原点的连线的斜率之积
是椭圆上不同两点,且这两点与坐标原点的连线的斜率之积 .(1)求椭圆
.(1)求椭圆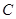 的方程;(2)求证:
的方程;(2)求证: 为定值,并求该定值.
为定值,并求该定值.
(本小题满分12分)某 公司购买了一博览会门票10张,其中甲类票4张,乙类票6张,现从这10张票中任取3张奖励一名员工.
公司购买了一博览会门票10张,其中甲类票4张,乙类票6张,现从这10张票中任取3张奖励一名员工.
(1)求该员工得到甲类票2张,乙类票1张的概率;
(2)求该员工得到甲类票1张数的概率,
(本小题满分10分)选修4—5 不等式证明选讲
已知 是不相等的正实数,求证:
是不相等的正实数,求证: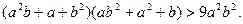
(本小题满分10分)选修4—4 参数方程与极坐标
求圆 被直线
被直线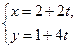 (
(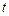 是参数
是参数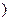 截得的弦长.
截得的弦长.
(本小题满分10分)选修4—1 几何证明选讲
在直径是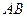 的半圆上有两点
的半圆上有两点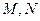 ,设
,设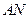 与
与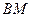 的交点是
的交点是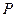 .求证:
.求证: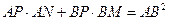
 |
(本小题满分12分)已知函数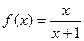 .
.
(Ⅰ)求函数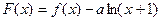 的单调递增区间;
的单调递增区间;
(Ⅱ)数列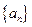 满足:
满足: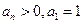 ,且
,且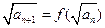 ,记数列
,记数列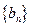 的前n项和为
的前n项和为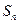 ,
,
且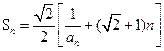 .
.
(ⅰ)求数列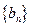 的通项公式;并判断
的通项公式;并判断 是否仍为数列
是否仍为数列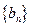 中的项?若是,请证明;否则,说明理由.
中的项?若是,请证明;否则,说明理由.
(ⅱ)设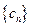 为首项是
为首项是 ,公差
,公差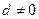 的等差数列,求证:“数列
的等差数列,求证:“数列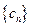 中任意不同两项之和仍为数列
中任意不同两项之和仍为数列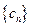 中的项”的充要条件是“存在整数
中的项”的充要条件是“存在整数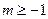 ,使
,使 ”
”