用总长为14.8米的钢条制成一个长方体容器的框架,如果所制的容器的底面的长比宽多0.5米,那么高为多少时容器的容器最大?并求出它的最大容积.
(本小题满分10分)
已知函数 、
、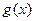 对任意实数
对任意实数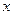 、
、 都满足条件
都满足条件
① ,且
,且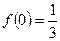 ,和②
,和②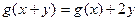 ,且
,且 ,
,
(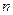 为正整数)
为正整数)
(Ⅰ)求数列 、
、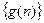 的通项公式;
的通项公式;
(II)设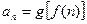 ,求数列
,求数列 的前
的前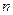 项和
项和 。
。
(本小题满分10分)
三角形ABC中,三个内角A、B、C的对边分别为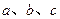 ,若
,若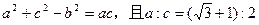 ,求角
,求角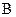 、角
、角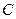 的大小。
的大小。
(本小题满分8分)
已知数列
 (
( )的前
)的前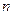 项的
项的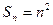 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若 ,记数列
,记数列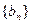 的前n项和为
的前n项和为 ,求使
,求使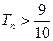 成立的最小正整数n的值。
成立的最小正整数n的值。
(本小题满分8分)
如图,A,B,C,D都在同一 个与水平面垂直的平面内,B,D为两岛上的两座
个与水平面垂直的平面内,B,D为两岛上的两座 灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为
灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为 ,
,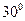 ,于水面C处测得B点和D点的仰角均为
,于水面C处测得B点和D点的仰角均为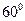 ,AC=0.1km。
,AC=0.1km。
(Ⅰ)试探究图中B,D间的距离与另外哪两点间距离会相等?
(II)求B,D间的距离。