如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(1)求证:AB1⊥面A1BD;
(2)求二面角A-A1D-B的余弦值;
(3)求点C到平面A1BD的距离.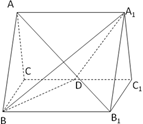
(本小题满分12分)已知 的面积是30,内角
的面积是30,内角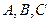 所对边长分别为
所对边长分别为 ,
, .
.
(Ⅰ)求 ;
;
(Ⅱ)若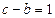 ,求
,求 的值.
的值.
已知数列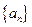 的各项均为正数,观察下面程序框图,当
的各项均为正数,观察下面程序框图,当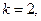
 时,分别有
时,分别有 和
和 。
。 (1)试求数列
(1)试求数列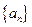 的通项;
的通项;
(2)若k=n时(n为正整数),求s的值(用n表示)。
假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:
 |
2 |
3 |
4 |
5 |
6 |
 |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
若由资料知,y对x呈线性相关关系,试求:
(Ⅰ)请画出上表数据的散点图;
(Ⅱ)请根据上表提供的数据,求出y关于x的线性回归方程 ;
;
(Ⅲ)估计使用年限为10年时,维修费用约是多少?
( )
)
为了让学生了解更多“社会法律”知识,
| 分组 |
频数 |
频率 |
| 60.5~70.5 |
1 |
0.16 |
| 70.5~80.5 |
10 |
2 |
| 80.5~90.5 |
18 |
0.36 |
| 90.5~100.5 |
3 |
4 |
| 合计 |
50 |
1 |
某中学举行了一次“社会法律知识竞赛”,
共有800名学生参加了这次竞赛. 为了解
本次竞赛成绩情况,从中抽取了部分学
生的成绩(得分均为整数,满分为100
分)进行统计.请你根据尚未完成并有
局部污损的频率分布表,解答下列问题:
(1)若用系统抽样的方法抽取50个样本,
现将所有学生随机地编号为000,001,002,…,799,试写出第二组第一位学生的编号;
(2)填充频率分布表的空格1234并作出频率分布直方图;
(3)若成绩在85.5~95.5分的学生为二等奖,问参赛学生中获得二等奖的学生约有多少人?
某商场设有会员卡,会员持卡消费都有一定的补贴,商场规定:购买物品不超过100元,补贴5%;购买物品超过100元而不超过5000元,补贴7%;购买物品超过5000元,补贴10%.画出输入消费 元时,输出商场补贴金额
元时,输出商场补贴金额 的程序框图.
的程序框图.