以点F1(-1,0),F2(1,0)为焦点的椭圆C经过点(1,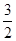 )。
)。
(I)求椭圆C的方程;
(II)过P点分别以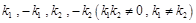 为斜率的直线分别交椭圆C于A,B,M,N,求证:
为斜率的直线分别交椭圆C于A,B,M,N,求证:  使得
使得
一个袋中装有形状大小完全相同的球9个,其中红球3个,白球6个,每次随机取1个,直到取出3次红球即停止.
(1)从袋中不放回地取球,求恰好取4次停止的概率P1;
(2)从袋中有放回地取球.
①求恰好取5次停止的概率P2;
②记5次之内(含5次)取到红球的个数为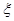 ,求随机变量
,求随机变量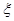 的分布列及数学期望.
的分布列及数学期望.
如图,四棱锥P—ABCD中,PD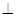 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD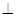 DC,AB=AD=1,DC=2,PD=
DC,AB=AD=1,DC=2,PD= ,M为棱PB的中点.
,M为棱PB的中点.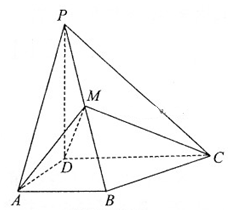
(1)证明:DM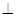 平面PBC;
平面PBC;
(2)求二面角A—DM—C的余弦值.
已知函数 的最小正周期是
的最小正周期是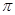 .
.
(1)求 的单调递增区间;
的单调递增区间;
(2)求 在[
在[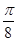 ,
, ]上的最大值和最小值.
]上的最大值和最小值.
设函数 的定义域是
的定义域是 ,其中常数
,其中常数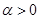 .(注:
.(注: 
(1)若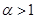 ,求
,求 的过原点的切线方程.
的过原点的切线方程.
(2)证明当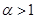 时,对
时,对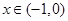 ,恒有
,恒有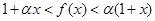 .
.
(3)当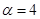 时,求最大实数
时,求最大实数 ,使不等式
,使不等式 对
对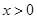 恒成立.
恒成立.
设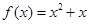 ,用
,用 表示
表示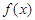 当
当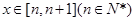 时的函数值中整数值的个数.
时的函数值中整数值的个数.
(1)求 的表达式.
的表达式.
(2)设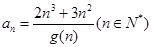 ,求
,求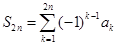 .
.
(3)设 ,若
,若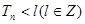 ,求
,求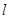 的最小值.
的最小值.