已知函数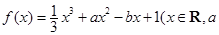 ,
,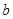 为实数)有极值,且在
为实数)有极值,且在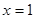 处的切线与直线
处的切线与直线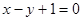 平行.
平行.
(Ⅰ)求实数a的取值范围;
(Ⅱ)是否存在实数a,使得函数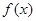 的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
(Ⅲ)设函数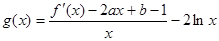 试判断函数
试判断函数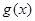 在
在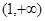 上的符号,并证明:
上的符号,并证明: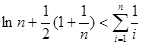 (
(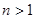 ).
).
已知函数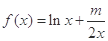 ,
,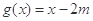 ,其中
,其中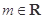 ,
, 为自然对数的底数.
为自然对数的底数.
(Ⅰ)当 时,求函数
时,求函数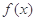 的极小值;
的极小值;
(Ⅱ)对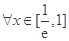 ,是否存在
,是否存在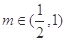 ,使得
,使得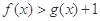 成立?若存在,求出
成立?若存在,求出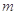 的取值范围;若不存在,请说明理由;
的取值范围;若不存在,请说明理由;
已知椭圆 :
: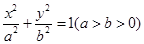 经过点
经过点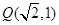 ,且焦点与双曲线
,且焦点与双曲线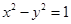 的焦点相同.
的焦点相同.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过点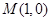 的直线
的直线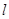 交椭圆
交椭圆 于
于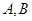 两点,交
两点,交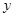 轴于点
轴于点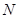 ,若
,若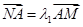 ,
,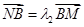 ,求证:
,求证: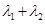 为定值.
为定值.
在中学生综合素质评价的测评中,分“优、良、不及格”三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并作出频数统计表如下:
(Ⅰ)从表二的非优秀学生中随机选取2人交谈,求所选2人中恰有1人测评等级为良的概率;
(Ⅱ)由表中统计数据填写下边 列联表,并判断是否有
列联表,并判断是否有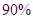 的把握认为“测评结果优秀与性别有关”.
的把握认为“测评结果优秀与性别有关”.
| 男生 |
女生 |
总计 |
|
| 优秀 |
|||
| 非优秀 |
|||
| 总计 |
参考数据与公式: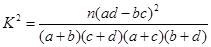 ,其中
,其中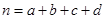 .
.
临界值表:
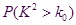 |
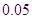 |
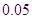 |
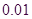 |
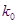 |
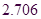 |
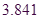 |
 |
已知侧棱垂直于底面的三棱柱 的所有棱长都相等,
的所有棱长都相等, 为棱
为棱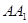 中点.
中点.
 (Ⅰ)证明:
(Ⅰ)证明: ;
;
(Ⅱ)在线段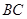 上是否存在点
上是否存在点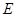 ,使
,使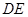 ∥平面
∥平面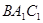 ,若存在,确定点
,若存在,确定点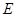 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
(本题满12分)已知A、B、C为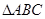 的三个内角且向量
的三个内角且向量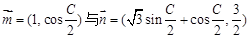 共线。
共线。
(Ⅰ)求角C的大小;
(Ⅱ)若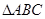 的外接圆面积为
的外接圆面积为 ,求三角形
,求三角形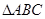 面积最大值.
面积最大值.