记关于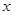 的不等式
的不等式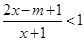 的解集
的解集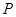 ,不等式
,不等式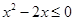 的解集为
的解集为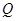 .
.
(1)若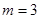 ,求集合
,求集合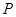 ;
;
(2)若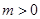 且
且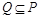 ,求
,求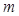 的取值范围.
的取值范围.
(本小题满分15分)
已知四棱锥 的底面为直角梯形,
的底面为直角梯形, ,
, 底面
底面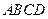 ,且
,且 ,
, ,
, 是
是 的中点。
的中点。
(Ⅰ)证明:面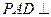 面
面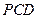 ;
;
(Ⅱ)求 与
与 所成的角;
所成的角;
(Ⅲ)求面 与面
与面 所成二面角的大小。
所成二面角的大小。
(本小题满分14分)
已知函数
(Ⅰ)写出函数的单调递减区间;
(Ⅱ)设 ,
,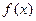 的最小值是
的最小值是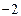 ,最大值是
,最大值是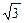 ,求实数
,求实数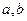 的值.
的值.
(本小题满分14分)
某商场在店庆日进行抽奖促销活动,当日在该店消费的顾客可参加抽奖.抽奖箱中有大小完全相同的4个小球,分别标有字“生”“意”“兴”“隆”.顾客从中任意取出1个球,记下上面的字后放回箱中,再从中任取1 个球,重复以上操作,最多取4次,并规定若取出“隆”字球,则停止取
个球,重复以上操作,最多取4次,并规定若取出“隆”字球,则停止取 球.获奖规则如下:依次取到标有“生”“意”“兴”
球.获奖规则如下:依次取到标有“生”“意”“兴” “隆”字的球为一等奖;不分顺序取到标有“生”“意”“兴”“隆”字的球,为二等奖;取到的4个球中有标有“生”“意”“兴”三个字的球为三等奖.
“隆”字的球为一等奖;不分顺序取到标有“生”“意”“兴”“隆”字的球,为二等奖;取到的4个球中有标有“生”“意”“兴”三个字的球为三等奖.
(Ⅰ)求分别获得一、二、三等奖的概率; (Ⅱ)设摸球次数为
(Ⅱ)设摸球次数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(12分)已知函数
(1)写出函数的单调递减区间;
(2)设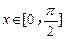 ,
,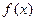 的最小值是
的最小值是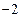 ,最大值是
,最大值是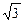 ,求实数
,求实数 的值
的值
(10分)如图,PA⊥矩形ABCD所在的平面,M、N分别是AB、PC的中点.
(1)求证:MN//平面PAD
(2)求证:MN⊥CD
(3)若∠PDA=45°,求证:MN⊥平面PCD.