已知函数f(x)=2ax-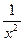 , x
, x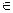
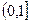 。
。
(1)若f(x)在x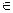
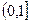 上是增函数,求a的取值范围;(2)求f(x) 在x
上是增函数,求a的取值范围;(2)求f(x) 在x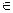
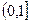 上的最大值。
上的最大值。
(I)已知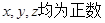 ,求证:
,求证: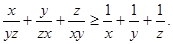
(II)已知正数a、b、c满足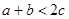 ,求证:
,求证: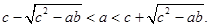
设M是由满足下列条件的函数 构成的集合:“①方程
构成的集合:“①方程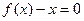 有实数
有实数
根;②函数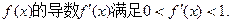 ”
”
(I)判断函数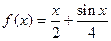 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(II)集合M中 的元素
的元素 具有下面的性质:若
具有下面的性质:若 的定义域为D,则对于任意
的定义域为D,则对于任意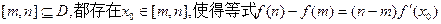 成立。试用这一性
成立。试用这一性
质证明:方程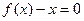 只有一个实数根;
只有一个实数根;
(III)对于M中的函数 的实数根,求证:对于
的实数根,求证:对于 定义
定义
域中任意的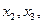 当
当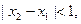 且
且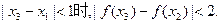
如图,ABCD是正方形空地,正方形的边长为30m,电源在点P处,点P到边AD、AB的距离分别为 9m、3m,某广告公司计划在此空地上竖一块长方形液晶广告屏幕MNEF,MN:NE=16:9,线段MN必须过点P,满足M、N分别在边AD、AB上,设
9m、3m,某广告公司计划在此空地上竖一块长方形液晶广告屏幕MNEF,MN:NE=16:9,线段MN必须过点P,满足M、N分别在边AD、AB上,设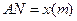 ,液晶广告屏幕MNEF的面积为
,液晶广告屏幕MNEF的面积为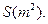
(I)求S关于x的函数关系式,并写出该函数的定义域;
(II)当x取何值时,液晶广告屏幕MNEF的面积S最小?
设函数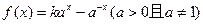 是定义域为R上的奇函数;
是定义域为R上的奇函数;
(Ⅰ)若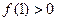 ,试求不等式
,试求不等式
 的解集;
的解集;
(Ⅱ)若 上的最小值。
上的最小值。