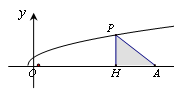
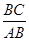如图,已知点 ,直线
,直线 与函数
与函数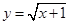 的图象交于点
的图象交于点 ,与
,与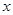 轴交于点
轴交于点 ,记
,记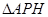 的面积为
的面积为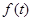 .
.
(Ⅰ)求函数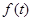 的解析式;
的解析式;
(Ⅱ)求函数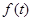 的最大值.
的最大值.
已知F1( 2,0),F2(2,0),点P满足|PF1|-|PF2|=2,记点P的轨迹为S,过点F2作直线
2,0),F2(2,0),点P满足|PF1|-|PF2|=2,记点P的轨迹为S,过点F2作直线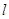 与轨迹S交于P、Q两点,过P、Q作直线x=的垂线PA、QB,垂足分别为A、B,记λ=|AP|·|BQ|.
与轨迹S交于P、Q两点,过P、Q作直线x=的垂线PA、QB,垂足分别为A、B,记λ=|AP|·|BQ|.
(1)求轨迹S的方程;
(2)设点M( 1,0),求证:当λ取最小值时,△PMQ的面积为9.
1,0),求证:当λ取最小值时,△PMQ的面积为9.
已知函数
(1)若x1=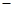 2和x2=4为函数f(x)的两个极值点,求函数
2和x2=4为函数f(x)的两个极值点,求函数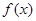 的表达式;
的表达式;
(2)若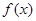 在区间[
在区间[ 1,3]上是单调递减函数,求
1,3]上是单调递减函数,求 的最小值.
的最小值.
如图,在三棱锥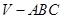 中,
中, 底面
底面 ,
, ,
, 是
是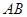 的中点,且
的中点,且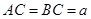 ,
,
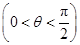 .
.
(1)求证:平面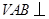 平面
平面 ;
;
(2)当角 变化时,求直线
变化时,求直线 与平面
与平面 所成的角的取值范围
所成的角的取值范围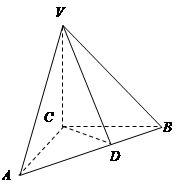
为了拓展网络市场,腾讯公司为QQ用户推出了多款QQ应用,如“QQ农场”、“QQ音乐”、“QQ读书”等.市场调查表明,QQ用户在选择以上三种应用时,选择农场、音乐、读书的概率分别为 ,
, ,
,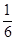 .现有甲、乙、丙三位QQ用户独立任意选择以上三种应用中的一种进行添加.
.现有甲、乙、丙三位QQ用户独立任意选择以上三种应用中的一种进行添加.
(1)求三人中恰好有两人选择QQ音乐的概率;
(2)求三人所选择的应用互不相同的概率.
已知函数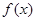
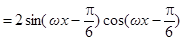 (其中
(其中 >0,
>0,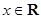 )的最小正周期为
)的最小正周期为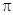 .
.
(1)求 的值;
的值;
(2)在△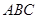 中,若A<B,且
中,若A<B,且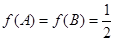 ,求
,求