直角坐标系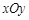 中,曲线
中,曲线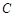 的参数方程为
的参数方程为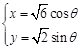 (
(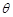 为参数),直线
为参数),直线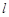 的参数方程为
的参数方程为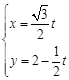 (
(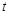 为参数),
为参数),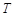 为直线
为直线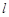 与曲线
与曲线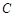 的公共点. 以原点
的公共点. 以原点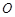 为极点,
为极点,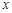 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(Ⅰ)求点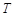 的极坐标;
的极坐标;
(Ⅱ)将曲线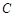 上所有点的纵坐标伸长为原来的
上所有点的纵坐标伸长为原来的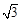 倍(横坐标不变)后得到曲线
倍(横坐标不变)后得到曲线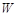 ,过点
,过点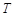 作直线
作直线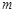 ,若直线
,若直线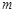 被曲线
被曲线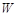 截得的线段长为
截得的线段长为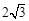 ,求直线
,求直线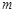 的极坐标方程.
的极坐标方程.
(本小题满分12分)已知命题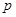 :方程
:方程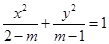 的图象是焦点在
的图象是焦点在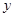 轴上的双曲线;命题
轴上的双曲线;命题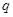 :方程
:方程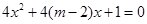 无实根;又
无实根;又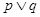 为真,
为真,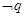 为真,求实数
为真,求实数 的取值范围.
的取值范围.
(本小题满分12分)一动圆和直线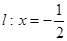 相切,并且经过点
相切,并且经过点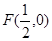 ,
,
(I)求动圆的圆心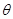 的轨迹C的方程;
的轨迹C的方程;
(II)若过点P(2,0)且斜率为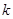 的直线交曲线C于M
的直线交曲线C于M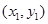 ,N
,N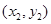 两点.
两点.
求证:OM⊥ON.
.(本小题满分12分)已知数列 的前
的前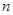 项和为
项和为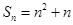 .
.
(I)求数列 的通项公式
的通项公式
(II)若 ,求数列
,求数列 的前
的前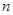 项和
项和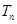
(本小题满分12分)已知 、
、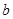 、
、 分别是△ABC中角A、B、C的对边,且
分别是△ABC中角A、B、C的对边,且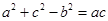 .
.
(I)求角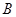 的大小
的大小
(II)若 ,求
,求 的值.
的值.
已知函数f(x)= (
(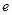 为自然对数的底数)⑴若
为自然对数的底数)⑴若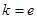 ,试确定函数
,试确定函数 的单调区间;⑵若
的单调区间;⑵若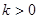 ,且对任意
,且对任意 恒
恒 成立,试确定实数
成立,试确定实数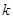 的取值范围.
的取值范围.