直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数),直线
为参数),直线 的参数方程为
的参数方程为 (
( 为参数),
为参数), 为直线
为直线 与曲线
与曲线 的公共点. 以原点
的公共点. 以原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(Ⅰ)求点 的极坐标;
的极坐标;
(Ⅱ)将曲线 上所有点的纵坐标伸长为原来的
上所有点的纵坐标伸长为原来的 倍(横坐标不变)后得到曲线
倍(横坐标不变)后得到曲线 ,过点
,过点 作直线
作直线 ,若直线
,若直线 被曲线
被曲线 截得的线段长为
截得的线段长为 ,求直线
,求直线 的极坐标方程.
的极坐标方程.
如图,一张平行四边形的硬纸片 中,
中,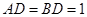 ,
, 。沿它的对角线
。沿它的对角线 把△
把△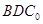 折起,使点
折起,使点 到达平面
到达平面 外点
外点 的位置。
的位置。
(Ⅰ)△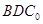 折起的过程中,判断平面
折起的过程中,判断平面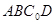 与平面
与平面 的位置关系,并给出证明;
的位置关系,并给出证明;
(Ⅱ)当△ 为等腰三角形,求此时二面角
为等腰三角形,求此时二面角 的大小。
的大小。
汶川震后在社会各界的支持和帮助下,汶川一中临时搭建了学校,学校餐厅也做到了保证每天供应1000名学生用餐,每星期一有A、B两样菜可供选择(每个学生都将从二者中选一),为了让学生们能够安心上课对学生的用餐情况进行了调查。调查资料表明,凡是在本周星期一选A菜的,下周星期一会有20%改选B,而选B菜的,下周星期一则有30%改选A,若用A 、B
、B 分别表示在第n个星期一选A、B菜的人数。
分别表示在第n个星期一选A、B菜的人数。
(1)试以A 表示A
表示A ;
;
(2)若A =200,求{A
=200,求{A }的通项公式;
}的通项公式;
(3)问第n个星期一时,选A与选B的人数相等?
已知向量 ,
,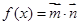 .
.
(I)若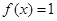 ,求
,求 值;
值;
(II)在 中,角
中,角 的对边分别是
的对边分别是 ,且满足
,且满足 ,求函数
,求函数 的取值范围.
的取值范围.
已知奇函数
(1)试确定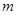 的值;
的值;
(2)若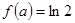 ,求
,求 的值;
的值;
(3)求函数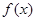 在
在 上的最小值.
上的最小值.
经过调查发现,某一时尚产品在投放市场的30天中,前20天其价格呈直线上升,后10天价格呈直线下降趋势。现抽取其中4天的价格如下表所示:
| 时间 |
第4天 |
第12天 |
第21天 |
第28天 |
| 价格(百元) |
34 |
42 |
48 |
34 |
(1)写出价格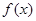 关于时间
关于时间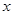 的函数表达式(
的函数表达式(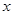 表示投放市场的第
表示投放市场的第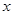 天);
天);
(2)若销售量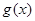 与时间
与时间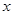 的函数关系式为:
的函数关系式为: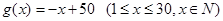 ,问该产品投放市场第几天,日销售额最高?
,问该产品投放市场第几天,日销售额最高?