如图,一张平行四边形的硬纸片 中,
中,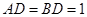 ,
, 。沿它的对角线
。沿它的对角线 把△
把△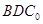 折起,使点
折起,使点 到达平面
到达平面 外点
外点 的位置。
的位置。
(Ⅰ)△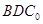 折起的过程中,判断平面
折起的过程中,判断平面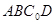 与平面
与平面 的位置关系,并给出证明;
的位置关系,并给出证明;
(Ⅱ)当△ 为等腰三角形,求此时二面角
为等腰三角形,求此时二面角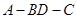 的大小。
的大小。
已知等差数列{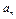 }前
}前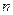 项和为
项和为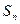 ,且
,且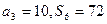
(Ⅰ)求数列{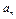 }的通项公式
}的通项公式
(Ⅱ)若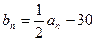 ,求数列
,求数列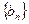 的前
的前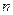 项和
项和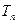
如图,已知斜四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD.
(1)证明:C1C⊥BD;
(2)当 的值为多少时,能使A1C⊥平面C1BD?请给出证明
的值为多少时,能使A1C⊥平面C1BD?请给出证明
在三棱锥 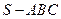 中,
中,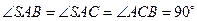 ,
,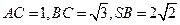 .
.
(1)求三棱锥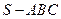 的体积;
的体积;
(2)求二面角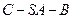 的大小;
的大小;
(3)求异面直线SB和AC所成角的余弦值。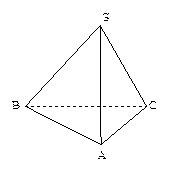
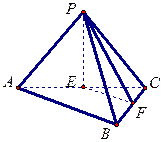
如图,在三棱锥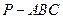 中,
中,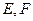 分别为
分别为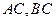 的中点。
的中点。
(1)求证: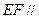 平面
平面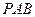 ;
;
(2)若平面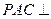 平面
平面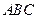 ,且
,且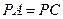 ,
,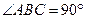 ,求证:平面
,求证:平面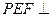 平面
平面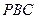 。
。
已知一个几何体的三视图如图所示。
(1)求此几何体的表面积;
(2)如果点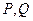 在正视图中所示位置:
在正视图中所示位置: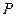 为所在线段中点,
为所在线段中点, 为顶点,求在几何体表面上,从
为顶点,求在几何体表面上,从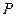 点到
点到 点的最短路径的长。
点的最短路径的长。