已知四棱锥E－ABCD的底面为菱形，且∠ABC＝60°，AB＝EC＝2，AE＝BE＝
，O为AB的中点．
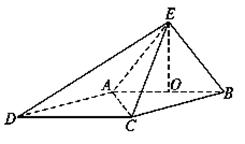
(Ⅰ)求证：EO⊥平面ABCD；
(Ⅱ)求点D到平面AEC的距离．
设函数
．
（1）解不等式
；
（2）若关于的不等式
的解集不是空集，试求
的取值范围．
（本小题满分10分）
如图，⊙O内切于△ABC的边于D，E，F，AB=AC，连接AD交⊙O于点H，直线HF交BC的延长线于点G。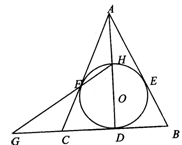
（1）求证：圆心O在直线AD上；
（2）求证：点C是线段GD的中点。
（本小题满分12分）
设函数
，其中
表示不超过
的最大整数，如
.
（1）求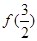
的值；
（2）若在区间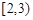
上存在x，使得
成立，求实数k的取值范围；
（3）求函数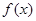
的值域.
已知函数
（1）若函数y=f(x)的图象切x轴于点（2，0），求a、b的值；
（2）设函数y="f(x)" 
的图象上任意一点的切线斜率为k，试求
的充要条件；（3）若函数y=f(x)的图象上任意不同的两点的连线的斜率小于1，求证
。
设函数
．
（1）若对定义域内任意
，都有
成立，求实数
的值；
（2）若函数
在定义域上是单调函数，求的范围；
（3）若
，证明对任意正整数
，不等式
都成立．